Evaluierung von Funktionswerten: Kostenfunktion? Integrale?

Hallo Community,


ich bin hauptsächlich im Gebiet der künstlichen Intelligenz unterwegs und mir fehlt aktuell leider ein wenig die Fantasie für eine spezifische, mathematische Problemstellung: ich habe ein System entwickelt, bei dem ich im Idealfall eine Wahrscheinlichkeitsverteilung als Ergebnis erhalte. Da der Idealfall in der Realität unwahrscheinlich ist, benötige ich eine "Bewertungsfunktion", die mir die Güte meiner Lösung approximiert.

Meine KI (Architektur kann ich bei Interesse gern erläutern, ist für die Problemstellung aber irrelevant), bzw. genauer spezifiziert ein künstliches neuronales Netz, trainiere ich mit dem Adam-Algorithmus und berechne den Fehler per Kreuzentropie.

Letztendlich - in der Praxis - berechne ich also den Fehler eines N-dimensionalen Ergebnisvektors wie folgt:



wobei y der Idealwert für den entsprechenden Eintrag und o der tatsächliche Wert im Ergebnisvektor an der i-ten Stelle ist.


Dieses Prozedere funktioniert zum Trainieren meines Systems gut. Allerdings würde ich gerne weitere Kostenfunktionen ausprobieren und/oder eine "unabhängige" Bewertungsfunktion haben.

Hier mal ein Plot (Ausschnitt!), wie der Idealfall (blau) aussehen würde und demgegenüber ein (künstlich) stark verrauschter Ergebnisvektor (rot):



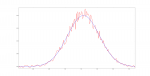
Der komplette Ergebnisvektor hat bei diesem Beispiel 1000 Dimensionen. Meistens arbeite ich mit Normalverteilungen, sodass die Summe eines idealen Vektors immer gleich 1 ist. In der Realität weicht die Summe des Vektors manchmal marginal von 1 ab, je nachdem wie der Erwartungswert und die Varianz der Normalverteilung gewählt ist. Da der Vektor ja eine Diskretisierung von der eigentlichen Dichtefunktion der Normalverteilung darstellt, ist z.B. wegen Rundungsfehlern von floats bei sehr großer oder sehr kleiner Varianz häufig die Summe marginal unterschiedlich von 1.

Kommen wir zur eigentlichen Fragestellung: Meine Problematik ist, dass ich gerne die Form der Kurven bewerten würde. Der Fehler, den ich per Kreuzentropie berechne, gibt mir ja nur die kumulierte "Abweichung" der einzelnen logistischen Fehler vom Idealfall/-vektor. Für das Trainieren des Netzes ist das wichtig, für meine Evaluation später aber nicht.
Da der Erwartungswert, also die Position meiner Gaußkurve in dem Ergebnisvektor, immer recht gut hinkommt, interessieren mich für die Evaluation hinterher alle Einträge, die mehr als ungefähr +/- 2 * Varianz entfernt von dem Erwartungswert liegen, nicht mehr. In der Grafik z.B. ist auch nur ungefähr das Interval [660, 800] interessant, der Rest des 1000D Vektors kann vernachlässigt werden.

Nun ist meine Problematik: wie evaluiere ich die Form der Gaußkurve?

Ich kann ziemlich zuverlässig ermitteln, welches Interval in dem Vektor am Ende interessant. Problematisch ist aber die weitere Methodik. Wenn ich hier wieder Kreuzentropie benutze, habe ich wieder "nur" die Abweichung von den einzelnen logistischen Fehlern. D.h. die Fehler sind nicht gleichmäßig gewichtet und ich verliere die Information darüber, ob die Form der Gaußkurve passt.
Fast noch schlimmer ist es, wenn ich ein Integral über das Interval bilde und dann das Integral vom Ergebnisvektor mit dem des Idealvektors vergleiche: wenn 50% des Intervals über dem Idealvektor liegt und 50% darunter und die Abweichungen ungefähr gleichmäßig darüber und darunter verteilt sind, dann bekomme ich bei einem Vergleich der Integrale natürlich nur einen marginalen Unterschied, obgleich der Ergebnisvektor relativ schlecht aussehen kann.

Auch mit absoluten oder quadratischem Fehler wird das ganze nicht besser.

Hat hier also eventuell jemand eine Idee, wie ich ein halbwegs zuverlässiges Maß finden kann, dass mir die Form der Gaußkurve beschreibt?
Ein Integral gibt mir halt nur eine gute Information darüber, ob die Fläche und damit die Wahrscheinlichkeit meiner Gaußkurve in dem gegebenen Interval "gut passt" im Vergleich zum Idealvektor. Es vernachlässigt aber, ob die Werte streng monoton steigend vor dem Hochpunkt und streng monoton fallend hinter dem Hochpunkt sind. Diese Form ist mir wichtig: bei starkem Rauschen kann die Gesamtwahrscheinlichkeit im Intervall zwar ganz gut hinkommen, aber die wenn die einzelnen Werte trotzdem wie in der Grafik so "hin und her springen", ist meine Monotonie stark verletzt: viele Punkte liegen direkt hintereinander über und dann wieder unter dem Idealwert.

Ich hoffe ich konnte meinen Gedankengang ungefähr darlegen


viele Grüße

ascer

du hast aber ein Maxima ( Hochpunkt ) der bekannt oder bestimmbar ist.

könntest daher ja das Intervall von rechts und links zum Hochpunkt betrachten

Weiterhin könntest auch die Steigungen in gewissen Intervallen berechnen und halt schauen ob sie ab und an stark fallen oder nur steigen.. je nach Intervall halt je kleiner desto genauer.

Du könntest Normalverteilungstests durchführen. Insbesondere der Lilliefors-Test argumentiert hier über die Form der Glockenkurve, welche mittels des dritten und vierten zentralen Moments (Schiefe und Kurtosis) beschrieben wird.

Ich bin etwas verwirrt. Die Form der Gausskurve wird doch anhand ihrer Parameter beschrieben.
https://upload.wikimedia.org/wikipe...PDF.svg/350px-Normal_Distribution_PDF.svg.png

Also, wir reden nur über die Funktion ohne Rauschen?
Eine Rauschmethode hast du schon gefunden?
Wenn du die Form der rauschfreien Funktion bewerten möchtest, wie würdest du die selber graphisch bewerten?

Ich hoffe ich habe das alles richtig verstanden.

wenn 50% des Intervals über dem Idealvektor liegt und 50% darunter und die Abweichungen ungefähr gleichmäßig darüber und darunter verteilt sind, dann bekomme ich bei einem Vergleich der Integrale natürlich nur einen marginalen Unterschied, obgleich der Ergebnisvektor relativ schlecht aussehen kann.

Zum Vergrößern anklicken....

Klar, wenns mal nach oben und mal nach unten abweicht ist die Summe ca 0. Daher dachte ich schon du würdest als 'Maß' der Qualität das Integral der Differenzfunktion - allerdings jeweils den absolutwert von y. Was ich dann aber nicht verstehe ist folgendes:

Auch mit absoluten oder quadratischem Fehler wird das ganze nicht besser.

Zum Vergrößern anklicken....

Das kann eigtl nicht sein? Mal abgesehen, dass ein Quadrat 2 starke Fehler stärker gewichtet als 1 schwachen (+1 aller Werte nicht vergessen, da für <1 ein quadrieren verkleinert), sorgt doch ein Quadrat durch -*-=+ dafür, dass du ähnlich wie bei abs() die Fehler 'Richtungsunabhängig' aufsummieren solltest.

Vielen Dank für die Beiträge!

Gerne noch mehr Vorschläge

xxMuahdibxx schrieb:

du hast aber ein Maxima ( Hochpunkt ) der bekannt oder bestimmbar ist.

könntest daher ja das Intervall von rechts und links zum Hochpunkt betrachten

Weiterhin könntest auch die Steigungen in gewissen Intervallen berechnen und halt schauen ob sie ab und an stark fallen oder nur steigen.. je nach Intervall halt je kleiner desto genauer.

Zum Vergrößern anklicken....

Jup, aber ein Integral ist leider noch keine optimale Idee, jenes hab ich ja schon versucht:

ascer schrieb:

Ich kann ziemlich zuverlässig ermitteln, welches Interval in dem Vektor am Ende interessant [ist] (...)
Ein Integral gibt mir halt nur eine gute Information darüber, ob die Fläche und damit die Wahrscheinlichkeit meiner Gaußkurve in dem gegebenen Interval "gut passt" im Vergleich zum Idealvektor. Es vernachlässigt aber, ob die Werte streng monoton steigend vor dem Hochpunkt und streng monoton fallend hinter dem Hochpunkt sind. Diese Form ist mir wichtig: bei starkem Rauschen kann die Gesamtwahrscheinlichkeit im Intervall zwar ganz gut hinkommen, aber die wenn die einzelnen Werte trotzdem wie in der Grafik so "hin und her springen"

Zum Vergrößern anklicken....

Ich kann zwar zusätzlich evaluieren, ob Monotonie gegeben ist, aber ein solcher boolescher Wert ist schwer für einen reellen Fehlerwert zu nutzen.

BAGZZlash schrieb:

Du könntest Normalverteilungstests durchführen. Insbesondere der Lilliefors-Test argumentiert hier über die Form der Glockenkurve, welche mittels des dritten und vierten zentralen Moments (Schiefe und Kurtosis) beschrieben wird.

Zum Vergrößern anklicken....

Daran hatte ich tatsächlich noch gar nicht gedacht. Das werde ich mal probieren, obgleich ich mir vorstellen könnte, dass auch dort hinterher die Schwierigkeit gegeben ist, einen reellen Fehlerwert zu ermitteln der mir quasi die Güte des Ergebnisvektors klassifiziert. Vielleicht in dem man immer gleich mehrere Nullhypothesen aufstellt und auf Ablehnung/Annahme prüft.

TheInterceptor schrieb:

Ich bin etwas verwirrt. Die Form der Gausskurve wird doch anhand ihrer Parameter beschrieben.
https://upload.wikimedia.org/wikipe...PDF.svg/350px-Normal_Distribution_PDF.svg.png

Zum Vergrößern anklicken....

In der Tat. Zu bestimmten Werten kenne ich ja auch (siehe blaue Kurve in meiner Beispielgrafik) den Erwartungswert und die Varianz, sodass ich eben jenen Idealvektor bestimmen kann.

TheInterceptor schrieb:

Also, wir reden nur über die Funktion ohne Rauschen?
Eine Rauschmethode hast du schon gefunden?

Zum Vergrößern anklicken....

Wir reden über die Evaluierung der Funktion mit Rauschen. Die Beispielgrafik besitzt "übertriebenes" Rauschen (um die Problematik zu verdeutlichen). Der Ergebnisvektor - also die daraus resultierende Funktion mit Rauschen - ist das, was die von mir erstellte künstliche Intelligenz als Ergebnis zu bestimmten Zeitpunkten t liefert.
Für bestimmte Trainingsdaten kenne ich die idealen Verteilungen, für Realdaten kann ich später - falls notwendig - manuell die idealen Verteilungen berechnen.

TheInterceptor schrieb:

Wenn du die Form der rauschfreien Funktion bewerten möchtest, wie würdest du die selber graphisch bewerten?

Zum Vergrößern anklicken....

Ich möchte die verrauschte Funktion bewerten. Dies tue ich zum Trainieren der KI per Kreuzentropie, was auch ganz gut funktioniert. Bei Realdaten hätte ich aber gerne eine zusätzliche Evaluierungsfunktion, die mir nicht ermittelt wie die Summe des logistischen Fehlers meiner Verteilung aussieht, sondern einfach die "Güte" des Ergebnisvektors.
Mich interessant da also z.B. nicht der ganze Vektor, sondern nur der "Aktivitätshügel", also grob alles +/- 2 * Varianz vom Hochpunkt aus gemessen...und dort eben die Form des Ergebnisvektors im Vergleich zu einem Idealvektor.
Bezüglich der Evaluation sollte z.B. (strenge) Monotonie gegeben sein: d.h. vor dem Hochpunkt sollte alle Werte steigend, danach fallend sein und nicht wie bei der verrauschten Beispielfunktion "willkürlich über oder unter" der Idealfunktion. Zusätzlich sollte "Breite" und "Höhe" des "Aktivitätshügels" vom Ergebnisvektor etwa dem Idealvektor entsprechen: d.h. Erwartungswert und Varianz sollten in etwa gleich sein bzw. die Funktionswerte im Intervall nicht zu stark abweichen.

Unter diesen Bedingungen würde ich gerne eine Abbildung finden, die diese Merkmale in die reellen Zahlen abbildet, sodass ich quasi eine "Güte-Evaluierungs-Funktion" erhalte.

kuddlmuddl schrieb:

Klar, wenns mal nach oben und mal nach unten abweicht ist die Summe ca 0. Daher dachte ich schon du würdest als 'Maß' der Qualität das Integral der Differenzfunktion - allerdings jeweils den absolutwert von y. (...)
Mal abgesehen, dass ein Quadrat 2 starke Fehler stärker gewichtet als 1 schwachen (+1 aller Werte nicht vergessen, da für <1 ein quadrieren verkleinert), sorgt doch ein Quadrat durch -*-=+ dafür, dass du ähnlich wie bei abs() die Fehler 'Richtungsunabhängig' aufsummieren solltest.

Zum Vergrößern anklicken....

Ja, ich habe in der Tat schon ein der Differenzfunktion mit absoluten Werten probiert, aber ebenso wie bei dem einfachen quadratischen Fehler oder dem absoluten Fehler ist die Problematik dabei, dass das Maß insgesamt dann zwar interessanter (als Summe) ist, d.h. für meine Wahrscheinlichkeitsverteilung kann ich ermitteln, ob die Gesamtwahrscheinlichkeit signifikant abweicht (verglichen mit dem Idealvektor), aber ich habe darin enthalten eben keine Information mehr über die "Form" der Kurve.

Was schön für eine Evaluierung wäre, wäre eben ein Maß welches mir verrät, wie "ähnlich" die ausgegebene Kurve zu der Idealkurve ist...also eben z.B. ob (strenge) Monotonie gegeben ist.
Umgangssprachlich: wenn ich einen stabilen, monotonen Ergebnisvektor von der KI bekomme, dann ist davon auszugehen, dass das Ergebnis relativ "robust" ist. In der Gesamtwahrscheinlichkeit (wenn z.B. alle Werte hier leicht über dem Idealvektor liegen) ist aber so ein Fehlerwert (Integrallösung, quadratischer Fehler, absoluter Fehler, ...) eventuell recht ähnlich zu einem Fehler, der einen verrauschten Ergebnisvektor hat (so wie die rote Kurve in dem Beispielplot). D.h. die Gesamtwahrscheinlichkeit wäre bei beiden ungefähr gleich falsch, aber in dem verrauschten Fall wäre das Ergebnis weniger robust.

Umgangssprachlich formuliert: ein verrauschter Ergebnisvektor impliziert weniger Robustheit, d.h. die KI hat zwar eventuell mit einem geringen Fehler klassifiziert, aber ist sich nicht "besonders sicher", das Ergebnis ist weniger reproduzierbar, sodass die Wahrscheinlichkeit von abweichenden Ergebnissen bei ähnlichen Eingaben höher ist.
Wenn die KI zwar knapp daneben liegt, aber sehr "saubere" Vektoren ausgibt (ordentliche Verteilung; Monotonie / wenig rauschen), dann ist der Fehlerwert eventuell sehr ähnlich, aber die Robustheit ist gegeben, sodass die Wahrscheinlichkeit von ähnlichen Ergebnissen bei ähnlichen Eingaben höher ist.
Selbstverständlich präferiere ich Letzteres ^^

Evtl habe ich dein Problem nicht ganz verstanden aber für mich hört sich der Kern des Problems nicht schwierig an.

Du möchtest generierte Funktionen (f) zueinander vergleichen und bewerten, welche 'ähnlicher' zu einer Normalverteilung ist, oder? Der Idealfall wäre eine exakte Gaussglocke (g).
Hierzu willst du jeder generierten Funktion eine Zahl (=Fehler) (F) zuordnen, der im Idealfall 0 ist?

Da stellt sich glaube ich vor allem die Frage welche Art von Ähnlichkeit dir persönlich für deine weitere Verwendung wichtig ist! Hierzu hab ich noch nicht genug rauslesen können um konkrete Vorschläge machen zu können.
Die Differenzfunktion f-g anzugucken ist natürlich ein naheliegender Ansatz. Dass hier aber unbedingt der Betrag d=abs(f-g) (anstatt direkt Integral/Summe) betrachtet werden muss ist ja klar.
Also zB F = Integral(d) oder F = Integral((1+d)^2).
Fehlerquadrate werden oft benutzt, weil sie eben dafür sorgen, dass große Abweichungen stärker bestraft werden als viele kleine - was je nach Anwendung oft auch Sinn macht? Ist das bei dir auch so?

Da deine anschließende Verwendung der 'besten' Funktion wahrscheinlich ja auch wieder mit Wahrscheinlichkeiten zu tun hat könnte es auch von großer Bedeutung sein, wo (für welches x) die Fehler liegen. Denn wenn zB die Mitte der Funktion häufiger verwendet wird als die Ränder könnte es Sinn machen jede Stelle der Differenzfunktion auch wieder mit einer Gausskurve zu gewichten. Also zB F = Integral((N*(1+d))^2)

Da du über monotonie schreibst hatte ich auch das versucht in Zahlen zu packen wo mir aber klar wurde, dass das eigtl durch die Fehlerquadrate auch abgedeckt wird, oder? Zumindest sofern - bis auf Rauschen - wieder eine Normalverteilung dahinter steckt.

Eine weitere Möglichkeit zu bewerten wäre Symmetrie. Also zunächst die Funktion f(mw - x) - f(mw + x) bilden und dann diese integrieren - wahlweise mit Quadrat oder ohne.

Mein Tipp: Nimm dir irgendwas 'handliches' (python, GnuPlot, matlab) und plotte dir verschiedene Kurven und überleg mit welcher Rechnung in der f und g vorkommen sich für 'gute Funktionen' kleine Zahlen ergeben und für 'schlechte funktionen' große Zahlen.
Wenn du mehr Bilder postest kann man da sicher leicht helfen.. Bei deinem bisher geposteten würde ich die oben vorgeschlagene 1+quadrat sache machen weil sich die starken Zacken sehr negativ auswirken.

bei R² also dem Bestimmtheitsmaß sind doch auch exponentielle funktionen unter excel z.b. möglich glaub bis x^6 damit kann man auch bestimmen wie genau die werte auf einer kurve liegen oder halt abweichen.

Da es R² ist werden ja auch nur positive flächen einbezogen.

oder man nutzt andere und bessere Statistikprogramme .

Wenn du Rauschen "bestrafen" willst, dann könntest du evtl. auch die Summe der absoluten Abweichungen der Steigungen zwischen jeweils aufeinanderfolgenden Punkten des Ergebnisvektors im Vergleich zum Idealvektor betrachten.

Sprich: du läufst durch die beiden Vektoren, ermittelst jeweils die Steigung und summierst die (abs) Abweichungen auf

Allerdings wird dadurch ne Verschiebung in y-Richtung ignoriert, d.h. du solltest noch mindestens ein weiteres Kriterium mit in die Bewertung einbeziehen, z.B. die 1+quadrat Sache die kuddlmuddl vorgeschlagen hat.