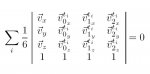Welche Bedeutung haben diese mathematischen Schreibweisen?

[Green Mamba]

Hallo,

ich bin hier in einem Paper auf mathematische Schreibweisen gestoßen, wie sie im Anhang dargestellt sind. Zum einen muss ich in Erfahrung bringen was der Betrags-Striche (die senkrechten Eingrenzungen der Matrix) bei der Matrizen-Darstellung zu bedeuten hat. Dabei kann man davon ausgehen dass jedes Element der Matrix eine normale Zahl ist. Es sind jeweils Verktor-Komponenten, aber das spielt eigentlich keine Rolle.

Zum anderen sind im zweiten Anhang um die Kreuzprodukte solche doppelten Betrags-Striche. Was haben diese zu bedeuten? Ist damit nur die Länge des Vektors gemeint, der sich zwischen den doppelten Strichen befindet, oder was sonst? Wird für die Vektorlänge normalerweise nicht einfach nur ein einzelner Betrag benutzt?
Ach ja, innerhalb der doppelten Betrags-Striche steht eigentlich nur ein Vektor. Vielleicht hilft das ja!?

Vielen Dank schonmal!

Schönen Gruß
Green Mamba

 

[Morgoth]

Das erste sieht für mich nach einer Determinante aus, zumindest schreibt man das so.

Beim zweiten würde ich auch wieder darauf tippen: wenn es sich bei a um eine Matrix handelt, dann bedeuten die inneren Betragsstriche die Determinante davon. Weil eine Determinante aber auch negatv werden kann, werden da nochmals Betragsstriche drumgesetzt.
Weil a wie Du sagst, nur ein Vektor ist, würde das die Schreibweise natürlich vereinfachen, aber allgemeiner ist das so.

Gruß
Morgoth

 

[Tommy]

Mit den Doppel-Betragsstrichen (also das zweite Bild von dir) ist die Norm des Vektors gemeint. In der Regel die Standard-Norm: Wurzel(<Vektorx,Vektorx>). Oder anders geschrieben: Wurzel(x1²+x2²+x3²+...+xn²).

 

[Green Mamba]

Ah, da kommen wir der Sache schon näher!
Hmm...
Wenn in der Matrix jetzt 4 Vektoren beinhaltet sind, v, v0, v1, v2, die alle zusammen einen Tetraeder bilden (Ortsvektoren), was sagt dann die Determinante aus? Ok, das ist jetz vielleicht ein bisschen viel verlangt, ich werd mal ein bisschen drüber grübeln, aber natürlich bin ich weiterhin für Tipps aller Art offen!

//Edit
Danke Tommy, das macht in dem Kontext sogar Sinn glaub ich, muss das aber mal noch nachprüfen. Hört sich auf jeden Fall verdächtig richtig an!

 

[Tommy]

Ist die Determinante null so
- ist das Volumen des von den Vektoren aufgespannten Parallelepipeds null
- sind die Spaltenvektoren der Matrix linear abhängig
- ist der Rang der Matrix nicht maximal
- Es muss also eine Vektorenhülle des Kerns geben

In Sachen Eigenwerte und Eigenvektoren möchte ich mich erst mal nicht aus dem Fenster lernen. Ein Eigenwert müsste null sein.

Bei dir steht aber ein Summenzeichen davor. Das ändert sie Sache natürlich etwas. Meine Aussagen beziehen sich auf die Determinante einer Matrix allgemein.

 

[Green Mamba]

Das Summenzeichen sagt nur aus, dass einen Summe über alle Tetraeder gebildet wird, ist also erst mal periphär. Ok, eine Null dürfte dann als Determinante niemals rauskommen, weil die Vektoren niemals linear abhängig sein können. Das geht aus dem Kontext hervor. Wichtiger wäre also ein Bezug zur größe der Determinante.


PS: Was bitte ist ein "Parallelepipeds"?

PPS: Tommy, bist ja richtig fit in Geometrie und Mathe! Hätt ich nicht erwartet!

//Edit
Ich habe jetzt die Bedeutung des Parallelepipeds herausgefunden, allerdings nur für 3 Vektoren die den Körper aufspannen. wie ist das dann mit vier?

 

[Tommy]

Klar bin ich da drin fit. Hab ja erst letztes Semster Klausur in Algebra geschrieben. Ein Parallelepiped ist im Zwei-Dimensionalen z.b ein Parallelogramm, im 3-Dimensionalen entsprechend ein Körper mit Tiefe (müsste sich Spat schimpfen) und so weiter.

Weitere Mathe-Fragen sind selbstverständlich willkommen.

 

[Green Mamba]

Aber klar, doch, habe noch so einige!
Ich hoffe die Klausur ist gut geworden!

Ok, dann kann man sich einen vierdimensionalen Parallelepid glaub ich nicht so einfach geometrisch vorstellen (Habe mal versucht das zu zeichnen, das poste ich lieber nicht! )
Aber ich denke aus dem Kontext heraus müsste es dann eigentlich so sein, dass die Determinante geteilt durch 6 dann das Volumen des Tetraeders beschreibt, der durch die 4 Orts-Vektoren beschrieben wird. (Hoffe ich mal zumindest)

Dann will ich gleich mal weiterfragen, das Kreuzprodukt zweier Vektoren stellt ja die Normale dar, die zu den beiden Vektoren passt. Aber wie lang ist der damit berechnete Normalen-Vektor? Wie steht das Verhältnis der Länge erzeugten Normalenvektors zu denen der einzelnen Vektoren? Oder hat die Länge gar was mit der durch die beiden Vektoren aufgespannten Flächeinhaltes zu tun?

PS: Hast du mal was von der fiesen Hesse-Matrix gehört? Die hat wohl irgendwas mit der konvexität von Oberflächen zu tun...

 

[LeChris]

Zum Ersteren:

Die Einsen sind nur Schmuckwerk (keine wirkliche Dimension), das 1/6 kann gleich weg. Wenn eine Determinante 0 ist, heißt das, daß v0, v1, v2 zum Zeitpunkt t(i) parallel zu v gerichtet (linear abhängig) sind.
Jetzt soll aber die Summe von vielen Determinanten Null sein...grübel...kann mir dann nur vorstellen, da ja v unabhängig von t(i) ist, dass sich v0,v1,v2 in ihrer "Summe" in Richtung v kompensieren.
Also: v geht direkt in den Schuhladen, v0,v1,v2 zusammen nach diversen Umwegen auch .

---

Zum Zweiten:

Das wird wohl der Betrag(Länge des Vektors) sein.

---

PS: 4-dimensionale Vorstellungen sind ähhh schwierig . Ein Volumen mit 4 Ortsvektoren gibt es nicht, es hat genau 3 .

 

[Green Mamba]

Naja, vielleicht hab ich mich mißverständlich ausgedrückt, die 4 Vektoren die in der Matrix stehen, beschreiben ja 4 Punkte im Raum. Verbindet man nun diese Punkte, so erhält man einen Tetraeder. Und um dessen Volumen geht es hier!
ist es möglich dass die Determinante das sechsfache des Volumens dieses Tetraeders beschreibt?

 

[LeChris]

Nein, der (4-dimensionale) Raum, den der Betrag der Determinante beschreiben würde, wäre jener, welcher von folgenden Vektoren aufgespannt würde:

1. vx, vy, vz, 1
2. v0x, v0y, v0z, 1
3. v1x, v1y, v1z, 1
4. v2x, v2y, v1z, 1

Ergo ein 4-dimensionaler Parallelepiped, kein Tetraeder oder irgendein anderer, minderwertiger, weil 3-dimensionaler Körper.

Ergo: höre auf, dir das vorzustellen .


Eine Determinante wäre: vx*v0y*v1z*1+v0x*v1y*v2z*1+v1x*v2y*vz*1+v2x*vy*v0z*1 -1*v0z*v1y*v2x-1*v1z*v2y*vx-1*v2z*vy*v0x-1*vz*v0y*v1x ...uff, 'hoffe habe mich nicht vertippt/-guckt

 

[Green Mamba]

Hmm...
Aber irgendeinen Zusammenhang zwischen dem durch die Determinante beschriebenen Volumen und dem Volumen des Tetraeder muss es geben, sonst fällt hier gleich mein ganzen Weltbild zusammen!

 

[LeChris]

Was für ein Tetraeder? Es gibt hier keins. v0,v1,v2 könnten ein "Span" aufspannen. Wenn dann v0,v1,v2 gleich lang wären, du diesen Span dann geeignet halbieren würdest, hättest du glaub' ich ein Tetraeder freak2.

EDIT: hey, der olle Smilie ist ja "f_reak2" statt ":f_reak2"

EDIT2: das mit dem Span halbieren vergesse mal wieder...finde vor lauter Schreck nicht mal eine Abbildung eines Spans =)

 

[Green Mamba]

Also nochmal langsam, es gibt in der Matrix oben im Anhang 4 Vektoren, v, v0, v1, v2. Diese werden als Punkte im Raum interprettiert. Drei der Punkte stellen ein Dreieck dar, wenn sie verbunden werden.
Soweit ja noch ganz einfach. Kommt jetzt der 4. Punkt, und werden die 3 anderen mit diesem jeweils verbunden, haben wir ... richtig, einen Tetraeder. Und um dessen Volumen gehts mir.
Ich hoffe ich konnte mich verständlicher ausdrücken!

 

[LeChris]

Hmmmm, hier hapert es an dem Verständnisses eines Vektors . Ein Vektor ist ein Pfeil, also ein Strich mit Dach an der einen Seite, kein Punkt.

So, das olle Ding ist gar nicht "Span", sondern Spat! Die drei Referenzseiten sind die Vektoren: http://mo.mathematik.uni-stuttgart.de/inhalt/aussage/aussage648/

 

[Green Mamba]

Ok, das ist ganz einfach, betrachte nur die Pfeilspitzen und vergiss den Pfeil im ganzen, dann sind es Punkte im Raum.
Es ist alles nur eine interprettationssache.

 

[LeChris]

Das ist das schöne an Mathematik: es ist kein Interpretationssache, sondern Definitionssache!

http://mo.mathematik.uni-stuttgart.de/inhalt/aussage/aussage71/

Ein Vektor ist bestenfalls die Strecke zwischen zwei Punkten, wenn du schon olle Punkte willst . Menschen sagen auch Pfeil .

---

Mal anders gefragt: Wenn ein Vektor ein Punkt wäre, wie könnte man dann die Länge/Betrag bestimmen?

---

Ohne jetzt mit Vektordefinitionen spammen zu wollen :

http://www.net-lexikon.de/Vektor-Mathematik.html
http://matheboard.de/lexikon/index.php/Vektor_(Mathematik)
(...)

 

[Green Mamba]

Ok, das ist eigentlich jetzt völlig irrelevant für mein Problem. Aber es gibt einen Unterschied zwischen Ortsvektor und Richtungsvektor. In meinem Fall sind es Ortsvektoren, und sollen als 3D-Koordinaten aufgefasst werden.
Ich möchte ja nur einen Beleg für meine Annahme des Zusammenhangs zwischen Tetraeder-Volumen und der Determinante.

PS: Das ganze Problem stellt sich für mich nicht als Mathematiker, sonder aus der Computergraphik heraus. Daher vielleicht auch mein mangelndes Bewusstsein für Definitionen.
Es ist eine frage mit praktischem Hintergrund.

 

[LeChris]

Den praktischen Hintergrund kenne ich ja leider nicht.

ABER: Die Determinante beschreibt den Spat(-volumen), kein Tetraeder o.ä.! Also muß ich deine Annahme widerlegen. Was die erste Gleichung beschreiben könnte, habe ich ja schon getippelt.

 

[Green Mamba]

Naja, aber es handelt sich ja auch nur um den 6. Teil des durch die Determinante beschriebenen Volumens, vielleicht passt das ja!?
Hat denn sonst niemannd eine Erklärung dafür? Vom Kontext her muss es eigentlich so sein.