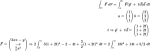[Physik]Arbeit ausrechnen

[MesserJack]

Hi Leute,

ich soll bei einer Übungsaufgabe einmal eine Arbeit über ein Integral errechnen und einmal Über die Potentialfunktion. Ich habe 2 Punkte gegeben (1,1,1) und (2,2,2) und F = (3xz-y,-x,3/2x^2)

Die Potenzial habe ich zuvor selbst ermittelt und V(x,y,z) = 3/2x^2z-xy
Wenn ich jetzt jeweils die Punkte einsetzte und abziehe habe ich 7,5 raus.

Jetzt müsste ich eigentlich über das Integral das gleiche heraus bekommen. Aber wenn ich es so mache, wie hier beschrieben http://mo.mathematik.uni-stuttgart.de/kurse/kurs18/seite21.html ,
nach ganz Unten scrollen, dann bekomme ich 131 raus, wenn ich von 1-2 intergriere. Und wie bekomme ich die Grenzen raus? Ich habe einfach mal 0-1 und 1-2 ausprobiert, aber beide male kommt nicht das richtige Ergebnis raus.

\int_{C}^{}~\vec{F}~d\vec{r} = \int_{a}^{b}~\vec{F}( \vec{p}~+~ t\vec{d})\vec{d}~ dt\\

a = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} 
b =\begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} \\

t\Rightarrow \vec{p}~+~ t\vec{d} = \begin{pmatrix} 1+2t \\ 1+2t \\1+2t \end{pmatrix} \\
\vec{F}= \begin{pmatrix} 3xz-y \\ -x \\ \frac{3}{2}x^{2}  \end{pmatrix}  
\Rightarrow 2\int_{b}^{a}~3(1+2t)^{2}-2-4t+\frac{3}{2}(1+2t)^{2}~dt  = 2\int_{b}^{a}~18t^{2}+14t+5/2~dt

http://www.matheboard.de/formeleditor.php

Könnt ihr mir helfen den Fehler zu finden, den ich mache. Ich mache es genau so wie in der Seite beschrieben, aber komme nicht auf die richtige Zahl. Ich habe den formeleditor von Mathboard benutzt.

 

[Plastikman]

Kannst du es vielleicht techen, dass ma auch wirklich lesen kann, was das alles heißen soll? ^^
Mit techen mein ich Latex. Wunderbares "Programm" zum schreiben phys/math. Formeln und Texte.

 

[Qqk]

Ich hoffe ich habe alles richtig verstanden. Mathe ist schon laaaange her.
Zunächst musst Du von a bis b integrieren. Das ist in Deiner Formel noch falsch.

Dann ist das doch eigentlich ganz einfach.
Du hast einen Startpunkt a mit (1,1,1) und eine Kurvenbeschreibung (1+2t, 1+2t, 1+2t)
Du Suchst also, für welches t (das ist dann ein a', weil a schon durch den Punkt a belegt ist) ein Punkt a=(1,1,1) "erreicht" wird.

1+2t=1
1+2t=1
1+2t=1

daraus folgt => 2t=0 => a'=t=0

Das gleiche nochmal mit dem Punkt b. Also für welches t (b') kommt man in der Kurve auf ("erreicht" man) b=(2,2,2).

1+2t=2
1+2t=2
1+2t=2

daraus folgt 2t=1 => b'=t=1/2

Deine Grenzen sind also t aus [a',b']=[0,1/2], dann kommst Du auch auf Deine 7,5.

hier nochmal das Integral:

...
=2*(18/3*t³+7*t²+5/2*t)
=2*(18/3*(1/2)³+7*(1/2)²+5/2*1/2)
=2*(0,75+1,75+1,25)
=2*(3,75)
=7,5

Alles klar?

 

[MesserJack]

@Plastikman: Ich habe einfach den Formeleditor von Matheboard benutzt. Das was ich dort reinkopiert habe, ist LaTeX. Und ich habe noch ein Bild eingefügt, falls jemand damit nichts anfgangen konnte.

Qqk: Jo das wars, ist richtig, ich wusste nie wie ich die Grenzen errechnen sollte. Dankte für die Hilfe.

Mfg
Micha