KomputerKarl
Cadet 1st Year
- Registriert
- Okt. 2025
- Beiträge
- 9
Moin,
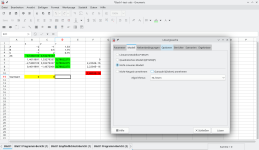
hat hier Jemand schonmal den Excel oder Libre Solver für ein Optimierungsproblem genutzt?
Ich habe selbst einen geschrieben (für OnlyOffice) und suche noch ein paar "echte" Beispiele, gerne kompliziert, um zu schauen wie gut, oder schlecht das ist und ein bisschen feintuning zu betreiben. 😃
VG Karl
hat hier Jemand schonmal den Excel oder Libre Solver für ein Optimierungsproblem genutzt?
Ich habe selbst einen geschrieben (für OnlyOffice) und suche noch ein paar "echte" Beispiele, gerne kompliziert, um zu schauen wie gut, oder schlecht das ist und ein bisschen feintuning zu betreiben. 😃
VG Karl