Algo zur Generierung einer Nachbarschaft nach bestimmten Regeln

[Krik]

Moin,

sorry für den langen Titel: Mir ist da echts nichts besseres eingefallen, was die Sache kürzer beschreibt.

Zur Ausgangssituation:
Ich will (später) eine 2D-Form generieren, die in mehrere ungefähr gleichgroße Flächen unterteilt ist. Dabei gilt, dass eine Fläche mindestens eine und maximal 6 (vllt. später auch 8) Nachbarflächen hat. Die Flächen sollen dabei von der Form her von unregelmäßigen Dreiecken bis Sechsecken (Achtecken) gehen (wenn möglich alle konvex). Natürlich sind die Flächen wild angeordnet, folgen also keiner Rasterstruktur oder ähnlichem.


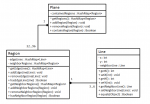
Ich habe mir dazu erst mal ein HashSet aus Objekten angelegt. Jedes Objekt steht für eine Fläche. Und jedes Objekt hat ein HashSet an Nachbarobjekte/-flächen.


Das Problem an der Sache mit der Nachbarschaftsgenerierung ist, dass bei einem naiven Algorithmus doofe Formen herauskommen können. zB hier liegen eine grüne und eine orange Fläche übereinander, beide sind Nachbarn der blauen Fläche:


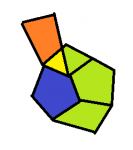
Ich hätte es gerne aber mosaikartig, ohne Überlappung.


Ist jemandem ein Algo bekannt, mit dem man das erreichen kann? Oder hab ich wieder Scheuklappen auf und sehe die einfache Lösung nicht?

Gruß Laurin

 

[Fireball89]

ich glaub es wäre ganz hilfreich, wenn du etwas Programmcode posten könntest.
Bei der Erstellung neuer Flächen, musst du doch eig nur die Schnittpunkte jeder Linie der neuen Flächen mit den Linien der alten Flächen analysieren. Schnittpunkte am Anfang- und Endpunkt einer Linie sind ok, aber mittendrin wäre ungültig.

Dann wäre die Modellierung interessant:
Teilen sind manche Objekte eine Linie? Oder sind diese "Anlegekanten" immer zwei "Linien-Objekte", die nur die gleichen Koordinaten haben?

 

[Krik]

Es gibt noch keinen Code. Ich stehe da noch ganz am Anfang. ^^

Ich bin mir auch noch nicht sicher, wie man hier am besten rangeht. Meine Idee ist es, eine Anzahl von (unbestimmten) Flächen vorzugeben und die dann irgendwie aneinander zu pappen.
Es wäre auch möglich, anderesherum anzufangen: Man nehme eine große, irgendwie geartete Fläche und zersäge sie in die angegebene Zahl von Flächen. Hier sehe ich aber das Problem, dass die Forderung nach annähernd gleichgroßen, konvexen Flächen nicht ohne großen Aufwand zu erreichen ist.


Die Modellierung weiß ich noch nicht. Das ergibt sich aus dem Algo. Jeder Fläche seine eigenen Begrenzungslinien halte ich aber für besser, was spätere Erweiterbarkeit angeht.

 

[Fireball89]

Ich würde mir da erstmal ein Klassendiagramm machen. Also hauptsächlich erstmal: Fläche und Linie
Und dann mal die ganzen Beziehungen zwischen diesen beiden Klassen einzeichen. Ich denke das hilft das Problem zu strukturieren.

 

[Krik]

Das Klassendiagramm würde bei mir etwa so aussehen:


Statt Randlinien könnte man auch Eckpunkte nehmen. Macht sich später vermutlich einfacher.



Ich sehe aber leider nicht, wie mir das weiterhilft.

 

[ice-breaker]

@Fireball89: Ein Klassendiagramm hilft ihm mal überhaupt nichts, wenn er ein Konzept für einen Algorithmus sucht


Also was du machen willst, hat scheinbar die Eigenschaft von Voronoi Diagrammen. Das ist ggf. sogar schon die Lösung oder?

 

[Krik]

ice-breaker, das scheint passend zu sein. Damit kann ich etwas anfangen.

So nach dem ersten Einlesen scheint die Größe der Flächen vor allem von den Seeds und ihren Abständen zueinander abzuhängen. Da muss ich mir noch was ausdenken, aber das bekomm ich sicher hin.

Vielen Dank!

 

[carom]

Mir wäre auch der Herr Woronoi eingefallen. Wenn ich jetzt nicht falsch liege, könnte es je nach Algorithmus aber schwierig werden, das ganze zu parametrisieren (was die minimale/maximale Anzahl an Eckpunkten angeht). Beim Fortune-Algorithmus z.B. verteilt man ja zunächst Punkte und läuft danach mit dem Algorithmus drüber. Nachdem die Punkte verteilt sind, ist das Diagramm aber eigentlich schon bestimmt und man kann die Beine hochlegen, d.h. die Zusammensetzung der Punktwolke bestimmt die späteren Formen. Da müsste man also erst mal die Punkte geeignet verstreuen.

Du könntest auch mittels Delaunay-Triangulation (da gibt's wiederum mehrere Algorithmen dazu) ein Netz aus lauter Dreiecken bauen (das ist gerade die Eigenschaft daran, es gibt nur Dreiecke). Danach könntest du über die Dreiecke iterieren und entsprechend Kanten löschen, so dass eben maximal n-eckige Formen entstehen. Was natürlich naiv ist, denn Dinge wegwerfen, die man zuvor berechnet hat, ist nicht sehr effizient.

 

[Fireball89]

@ice-breaker:
Tja, gut, dass du so genau weißt wie der TE denkt. Denn ich strukturiere mein Problem erstmal, bevor ich mir Algorithmen überlege. Ich finde das hilft ungemein. Es soll auch kein fertiges Klassendiagramm sein, sondern mehr ein Modell des Problembereichs. Dass es da schon Algorithmen gibt, wusste ich nicht.

 

[carom]

Ein Klassendiagramm hat an dieser Stelle trotzdem nichts verloren. Bei einem Algorithmus willst du eine Handlungsvorschrift oder Abfolge von Operationen finden, keine Struktur festlegen wie es ein Klassendiagramm macht. Ein Klassendiagramm ist außerdem schon viel zu nahe an einer konkreten Lösung, da es den Kontext auf die Objekt-orientierte (oder zumindest "Klassen-orientierte") Welt legt. Dem Algorithmus sollte es jedoch egal sein, wie er in Code gegossen wird, der weiß nicht, was Klassen sind.

 

[Krik]

Ist schon ok, ihr zwei. Jeder hat seinen eigenen Weg, an Probleme heranzugehen.


Lloyds Algo sieht recht passend aus. Ich gebe einfach eine irgendwie geartete Fläche vor, in der ich zufällig Punkte verteile. Der Algorithmus berechnet dann die Voronoi-Zellen und wichtet sie nach Flächeninhalt. Und das iteriert er ein paar Mal, bis die Flächeninhalte aller Zellen innerhalb eines definierten Wertebereiches liegen.
Das kostet zwar viel Rechenleistung, aber das ist in Ordnung, da es nur einmal am Beginn des Programms gemacht werden muss. Wenn der Computer es schafft, so ein Mosaik mit bis zu 96 Zellen in weniger als 10 Sekunden zu errechnen, bin ich zufrieden.

 

[maxwell-cs]

das geht mit deutlich mehr punkten in sekundenbruchteilen.

das berechnen des voronoi-diagramms in jeder iteration geht in O(n log n), das bestimmen der neuen punkte dürfte jeweils in linearzeit gehen, wenn ich mich gerade nicht irre.

 

[sash2k2]

Das ist ja mal ein super Thread! Ich wollte eigentlich nur noch Folgendes anmerken: Wenn du das Voronoi-Diagramm einer Punktmenge hast, dann entspricht der duale Graph der Delaunay-Triangulation. Ich erwähne es deshalb, da eine solche Triangulation alle deine gestellten Bedingungen erfüllt. Natürlich hättest du dann nur Dreiecke als Regionen, was sich aber leicht durch Verschmelzen benachbarter Regionen lösen lassen würde. Vielleicht bist du ja ein bisschen experimentierfreudig ...

Hier ist übrigens ein schönes Applet, mit welchem man den beschriebenen Zusammenhang nochmal selber ausprobieren kann.

 

[Krik]

Ich habe schon was gefunden, sash2k2.
Das erfüllt fast alle meine Wünsche, ist sauber programmiert und kann ich ohne Verrenkungen in mein Programm übernehmen.

Nur der theoretische Kram ist mir noch nicht in jedem Punkt klar. ZB ist mir noch unklar, wie man ermittelt, von wo bis wo die Grenzlinien gehen. Klar, sie gehen von Knotenpunkt bis Knotenpunkt, aber die Auswahl welche zwei Knotenpunkte verbunden werden müssen, hab ich noch nicht gerafft.
Aber das bekomm' ich noch auf die Reihe. Vom Prinzip her sind das Voronoi-Diagramm und die Delaunay-Triangulation eigentlich sehr einfach.

Tja, und Lloyds Algorithmus muss ich auch noch implementieren. Aber das schiebe ich noch auf, bis ich das andere komplett verstanden habe und ich auch privat wieder etwas mehr Zeit für dieses kleine Projekt habe. Es stehen bald wieder Prüfungen an und ich habe auch noch ne Menge Zeugs im Vorfeld abzugeben. Eigentlich schade, da ich viel lieber an diesem Projekt weiterarbeiten will, statt irgendwelche theoretischen Ausarbeitungen zu machen.

Gerade die Delaunay-Triangulation erlaubt es, eine Tesselation ähnlich dem, was moderne Grafikkarten können, zu realisieren. Da juckt es mich schon in den Fingern.


Trotzdem ein Dankeschön für deine Antwort.

 

[maxwell-cs]

spezialfälle mal außen vor ist die regel, welche punkte verbunden werden, doch einfach: wenn die voronoi-regionen zweier punkte eine gemeinsame kante haben, werden die punkte verbunden (dualer graph).

 

[Krik]

Da hätte ich auch selber drauf kommen müssen.