Java 3D-Bilder

[KadOros]

Hi,

Ich hoffe ich finde hier Hilfe.
Also ich möchte von einem Objekt ein 3D-Modell erstellen.
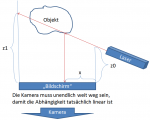
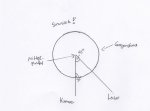
Dazu hab ich von dem Objekt 360 Bilder gemacht (einmal rundherum), dabei hab ich das Objekt mit einem Laser(Linienlaser) "bestrahlt". Ich hab jetzt also 360 Bilder vom Objekt, jeweils 1 Grad gedreht und mit einem Laser bestrahlt. Wie gehts jetzt aber weiter? Ich hab mir gedacht, als nächstes sollte ich eine Punktewolke erstellen.
Dafür hab ich die Roten Pixel (vom Laser) in einem 3 Diminsionalen Feld gespeichert
Feld[<id des Bildes>; <x-koordinaten>; <y-Koordinaten>]
Leider hab ich jetzt keine wirkliche idee wie ich weiter machen soll, hat jemand evtl. einen kleinen Denkanstoß für mich?

 

[Hancock]

Jetzt mit dem Feld die aktuelle Position berechnen, das sollte gehen (Vektorrechnung).

Dann kannste dir die Punktewolke ja schon zeichnen lassen (OpenGL).
Wenn du daraus jetzt n richtiges Modell machen willst wirds schwer, da dafür die Lösung nicht trivial ist.

 

[KadOros]

Ok werde mir die Vektoreinrechnung anschauen , danke für den Hinweis!
Ja soll schon ein richtiges Modell werden da
Ich das Objekt dann mit einem 3D-Drucker ausdrucken muss.

 

[KadOros]

Keiner eine , Idee ich komm leider nicht weiter?

 

[kuddlmuddl]

Das ist ein hochkomplexes Thema.. bei mir an der Uni gabs Info-Projekte die sich genau mit diesem Thema beschäftigt haben.
Erstmal ne grundsätzliche Frage:

Ich hab jetzt also 360 Bilder vom Objekt, jeweils 1 Grad gedreht und mit einem Laser bestrahlt

Dh in jedem Bild ist nur eine einzige rote Linie zu sehen? Eigtl müsstest du das Objekt doch zB von oben bis unten in jedem Bild abfahren? Sonst hast du ja nur eine einzige Höhe je Bild gescannt.
Kannst du mal 1, 2 Bilder posten?

Es gibt grundsätzlich 2 große Probleme:
1) Das Korrespondenz-Problem: Welcher Punkt in Bild n stimmt mit welchem Punkt in Bild n+1 überein
Hierbei gibts die Probleme, dass:
- nie die selben Objektpunkte in Bildpunkten abgebildet werden
- einige Punkte nur in Bild n und andere nur in Bild n+1 gesehen werden können da das Objekt auf sich selbst schatten wirft - selbst bei einer Kugel.

2) Die 3D-Informationen je Bild widersprechen sich.
Dh selbst wenn du in einer Folge von i Bildern jedesmal einen Punkt identifizieren konntest der wandert und selbst wenn der real unmögliche Fall eingetreten wäre dass sich dein Objekt immer um genau die selbe Achse gedreht hat und selbst wenn die Drehung immer um genau 1° stattgefunden hat: Selbst dann wirst du durch optische Ungenauigkeit die Position dieses einen Punkt im Raum nicht exakt kennen da bei jeder Messung andere Werte herausgekommen sind. Hierfür nutzt man häufig den Kalman-Filter. Aber den würde ich mir erstmal ersparen... der erhöht nur die Genauigkeit. Du könntest ja auch einfach nur Mitteln

 

[Hancock]

Wenn du die Positionen schon hast, kannst du einfach ne Wolke erstellen, also einfach alle Bildpunkte rein.
Dann ein Punkt in der Mitte nehmen und langsam "Füllen", also das VOlumen füllen und wenns dann an Bildpunkte der Wolke stößt (ala in der Umgebung ist ein Punkt), dann aufhören, dadurch müsstest du dann ein einigermaßen genaues Volumenmodell bekommen.

 

[Krik]

Was hast du denn eigentlich exakt für Daten? Richtung + Abstand vieler Punkte vom Laserursprung?
Da fällt mir nur ein, die Punktkoordinaten zu errechnen, damit man eine Punktwolke erstellen kann. Anschließend gehst du mit einem Algorithmus drüber, der benachbarte Punkte zu Polygone verbindet. Das Ergebnis kann aber viele Fehler haben, da benachbarte Punkte nicht zwangsweise ein Polygon bilden sollten, also nichts miteinander zu tun haben.

So oder so, der Computer wird die maximal eine Näherung auswerfen, die man dann per Hand nachbearbeiten darf.

 

[KadOros]

hi

Danke schonmal für die zahlreichen Hilfestellungen!

Das das Ergebniss nicht perfekt sein wird, ist mir klar und auch nicht sehr schlimm. Denn es handelt sich um ein Schulprojekt, da ist mehr der Weg das Ziel, solange das Endprodukt einigermaßen erkenbar ist, ist alles ok.
So jetzt zu den Daten die ich habe, ich habe die "Positionen" der "Objekte"(Kamara, Objekt, Laser), also die Winkel die sie zueinander haben. Außerdem hab ich die Koordinaten(x und y) der "rotesten" Punkte.
Wenn ich das richtig verstanden hab brauch ich jetzt den z-wert(Tiefe?) der Punkte für die Punktwolke?

Im Anhang hab ich mal 2 Bilder gepackt.

 

[kuddlmuddl]

täuscht das oder ist das Objekt vollständig Rotationssymetrisch? Darf diese Eigenschaft ausgenutzt werden? Das würde vieles vereinfachen

 

[KadOros]

Ja ist es, aber es ist leider nicht erlaubt das auszunutzen^^

 

[Hancock]

z werte für ein roten Laserpunkt:
z ist linear abhängig von der x-Koordinaten des Punktes
also
f:[-1,1]->[z0,z1]
f(x)=z
=>
z=ax+b, a € |R
a = (z1-z0)/2
b = z0

Ich hoffe du verstehst, was ich damit sagen will.

 

[Krik]

Ich glaube nicht, dass er das versteht.
Wenn er Schüler ist, dann kann er mit Vektorräumen noch nichts anfangen. *auf-f:[-1,1]->[z0,z1]-schiel*


Also, die Distanz zwischen Objekt und Kamera ist bekannt? Strahlt der Laser um 90° zur Kamera um das Objekt herum versetzt? Also:

Wenn ja, dann ist das gut, dann ist die rote Linie ein Meridian. Du hättest dann also 360 Meridiane, die du dann immer nur um 1° gedreht an der selben Stelle aufstellt.
Du bräuchtest dann nur etwas Trigonometrie, um die Koordinaten der einzelnen Punkte auf dem Meridian zu berechnen:
c = Abstand Kamera und Punkt auf dem Meridian
b = Abstand Zentrum des Objekts und Punkt auf dem Meridian
a = Abstand Kamera und Zentrum des Objekts
=> Phytagoras

Die nötigen Berechnungen für die Punktwolke solltest du jetzt eigentlich alleine herausbekommen können.

 

[Hancock]

e-Laurin:
So einfach ist das glaub nicht.
Wie auf den Bildern erkennbar ist, ist der Laser nicht senkrecht zur Kamera ausgerichtet.
Auch ist ja gerade der Winkel des Laserstrahls, der in die Kamera, fällt von Bedeutung.

Mein Lösungsansatz/-vorschlag wäre folgender:

bestimme, welchen Abstand der Punkt, der genau am rechten Rand vom Bild erfasst wird, zur Kamera hat sowie der linkeste Punkt. Diese beiden Werte nenn ich z0 (der rechte) und z1 (der linke).

Nun nimst du Bilbearbeitungssoftware oder ein eigenen Algorithmus, welcher dir die Koordinate jedes Laserpunktes entlang der y-Achse ausspuckt. Dieser x-Wert steht dann für den Abstand dieses Punktes von der Kamera (und liegt zwischen z0 und z1). Wenn ich jetzt annehme, das die x-Koordinaten von links nach rechts im Bereich von [0,1] liegen, dann ist die Entfernung von der Kamera und diesem Punkt gegeben durch z=z0+x*(z1-z0). Allerdings gilt das nur näherungsweise, wegen der Perspektive (bei einem Weitwinkelobjektiv ist die Abweichung größer als bei einem Zom auf das Objekt). Wenn ich an meine Rechner sitzt kann ich dir ne Zeichnung machen.

EDIT:
Hier das Bild, hoffentlich verständlich, wenn die Kamera näher kommt, wird die Abweichung durch die Verzerrung des Bildausschnittes immer größer.

 

[KadOros]

Hallo

Danke nochmal an alle die sich die Mühe machen mir zu helfen, top!

@e-Laurin
Leider ist der Laser nicht im 90° Winkel zur Kamera, sonder im 45° Winkel, 90° wären glaube ich aich nicht realisierbar, weil man dann die Laserlinie nicht auf dem Bild sehen würde.

@Hancock
Besonderen dank nochmal an dich für den Lösungsansatz! Klingt alles sehr einleuchtent, ich versuche deinen Ansatz am Donnerstag(der einzige Tag, an dem ich Zugriff darauf habe -.-) in Java umzusetzen.

 

[KadOros]

Hallo nochmal

Ich bin nicht wirklIch weiter gekommen.
Ich Fang mal von vorne an. Ich will mit Java eine stl Datei erstellen mit der ich mit einem 3d Drucker das Objekt "nachdrucken" kann. Dafür muss ich ein 3D- Modell meines Objekts erstellen. Das will ich anhand der roten Pixel des Lasers machen. Ich brauche also die 3D Koordinaten der Pixel, im Koordinatensystem gesehen x y und z. X und y der relevanten Pixel gab ich schon jezt fehlt noch z (Entfernung des Objekts von der Kamera oder dem Laser?) . Ich hab's mit Hancocks Lösungsansatz versucht, dass hat aber nicht wirklIch geklapt. Ich habe jetzt den Hinweis sinussastz bekommen? Hab aber kine Idee wie i h das umsetzte, hab Au h eine Skizze gezeichnet die ich hochladen werde wenn i h Zuhause bin. Ich hoffe jemand kann mir da ein bisschen helfen

 

[Hancock]

z ist das, was du dir definierst...

Hast du denn ein paar Bilder von der Kamera vorliegen, weil dann könntest du auch daheim daran weiterprogrammieren...

 

[KadOros]

Ja die 2 die ich oben gepostet habe habe ich auch Zuhause.

Hier mal eine Skizze vom Scanner + Objekt und die für den Sinussatz.
Außerdem hab ich ja die Information das sich das Objekt pro Bild um 1 Grad dreht.
Nur weiß ich nicht wirklich wie ich davon auf z komme.

 

[Hancock]

Also das Scannerbild ist ja mal nicht so groß^^.

Die Zeichnung vernachlässigt ein Aspekt, nähmlich den Lichtstrahl, den du später siehst.

Du brauchst Abstand a und b als Entfernung von der Kamera zum rechtesten und linkesten Lasterpunkt, der noch drauf ist, den Winkel der aktuellen Aufnahme (also um wie viel gedreht) Phi.
Dann gilt:

Kameraposition.x=cos(phi);
Kameraposition.y=sin(phi);
Kameraposition.z=Konstant;
Blickrichtung = normalize( sin(phi), cos(phi), 0);
for(int i=0;i<laserpunkte.size();++i){
distance=a+laserpunkte[i].v*(b-a);
punkt=Kameraposition+Blickrichtung*distance+Sphärische_Korrektur(laserpunkte[i].position);
}

 

[KadOros]

ok, dass hilft mir schon weiter danke!
Die Frage ist jetzt nur wie ich an a,b und v komme.
Außerdem was ist die Sphärische_Korrektur?

Im Anhang nochmal ein größeres Bild vom Scanner aufbau

 

[Hancock]

a und b musst du ausmessen.
v ist die relative Größe zwischen 0 und 1, die du aus der Auswertung der Bilder bekommen hast.
Mit sphärischer Korrektur mein ich den Umstand, dass die Entfernung von der Kamera ja nicht allein dann den Weltpunkt angibt, sondern auch noch von all den anderen Parametern abhängt. Also vor allem von dem Winkel, wie er in die Kamera trifft, wechen du aber wiederum aus den Koordinaten des Bildpunktes extrahieren kannst. Also Alles in Allem nicht so schwer, aus dem ersten Schritt folgt der zweite und so weiter.

Dein größtes Problem wird sein, aus der Punktewolke dann ein massives 3D-Modell zu erstellen.