Brückenrätsel Lösung?

[Scorb]

Also, ich habe hier ein Rätsel, welches ich partout nicht gelöst bekomme. Es soll aber angeblich eine Lösung geben. Also folgendes Problem:

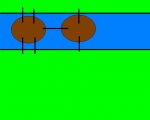
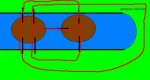
Es gibt 2 Brücke, die miteinander verbunden sind. Nun möchte ein Tourist über jeden Brückenabschnitt gehen. Er ist jedoch faul, und möchte jede Brückenabschnitt (insgesamt 7 Stück) (Fussweg/ Straße oder was immer auch) nur 1x! benutzen.
Welchen Weg muss er gehen?
Schlauchbote, Hubschraueber oder ähnliches sind nicht erlaubt. Der Startpunkt ist egal!

Danke
Scorb

 

[m@Go0]

Ich rätsel da auch gerade schon, aber bist du dir sicher dass es dort eine Lösung gibt ?
Ich find bis jetzt noch keine, aber vlt. werd ich sie ja noch finden ^^
edit: Jetzt hab ich eine Lösung, aber nur, wenn man rechts oben beim Bildende wieder Linksoben herauskommt *g*

 

[13thAngel]

Ich rätsel da auch gerade schon, aber bist du dir sicher dass es dort eine Lösung gibt ?
Ich find bis jetzt noch keine, aber vlt. werd ich sie ja noch finden ^^
edit: Jetzt hab ich eine Lösung, aber nur, wenn man rechts oben beim Bildende wieder Linksoben herauskommt *g*

poste doch mal nen veränderten screenshot mit dem weg, plz!

 

[IRID1UM]

also ich glaub, das ist so ein verarschungsrätsel bei dem es gar keine lösung gibt. so wie folgendes:
man hat drei häuser und ein e-werk, gas-werk und wasserwerk (siehe skizze). alle drei häuser müssen mit strom, gas und wasser verbunden werden, ohne dass sich die leitungen kreuzen.
mfg
IRID1UM

 

[Mr. Snoot]

edit: Jetzt hab ich eine Lösung, aber nur, wenn man rechts oben beim Bildende wieder Linksoben herauskommt *g*

Und wieso gehst dann nicht gleich nah links? Da ist doch keine blokade die man umgehen muss

Ich glaub ja sowieso, dass das ein ganz anderes Rätsel ist: Lege ein Streichholz um damit die Gleichung stimmt

@ IR1D1UM: da gibt's aber doch ne Lösung

 

[WingX]

Das Problem ist die Mathematik.
Solange eine der Brücken eine ungerade Anzahl an Zugängen hat, kann man sich auf den Kopf stellen, man findet keinen solchen Weg, Weil man auf einer Brücke immer hängenbleibt.
Leonhard Euler hat das im "Königsberger Brückenrätsel" schon beschrieben.

 

[th3o]

hier hat jede brücke eine ungerade anzahl an zugängen. die eine 5 die andere 3.

ausschnitt: Sie waren das Wahrzeichen von Königsberg und wurden vor allem dadurch berühmt, daß der große Schweizer Mathematiker Leonhard Euler sie als "Königsberger Brückenrätsel" 1736 in das damals neue Gebiet der Topologie einbrachte. Es wird noch heute an in- und ausländischen Universitäten in den Lehrstoff einbezogen, denn das Rätsel ist ein Rätsel geblieben: es ist unlösbar.

Ausgedacht hat er es nicht. Das hatten die Königsberger bereits hundert Jahre vor ihm getan, als die Honig-Brücke gebaut worden war. Im 17. Jahrhundert war es für sie ein beliebtes Spiel zu untersuchen, ob man die sieben Brücken passieren könnte, ohne sie zweimal zu beschreiten. Viele werden dies versucht haben, vergeblich, wie Euler dann wissenschaftlich bewies.

 

[Scorb]

also ich glaub, das ist so ein verarschungsrätsel bei dem es gar keine lösung gibt. so wie folgendes:
man hat drei häuser und ein e-werk, gas-werk und wasserwerk (siehe skizze). alle drei häuser müssen mit strom, gas und wasser verbunden werden, ohne dass sich die leitungen kreuzen.
mfg
IRID1UM

Im 3dimensionalen Raum gehts

 

[Rockzentrale]

Im 3dimensionalen Raum gehts

Wenn man es auch einen Baltt Patier versucht ist es NICHT möglich

Ich und 15 andere Leute + Lehrer haben uns über dieses Rätsel ein ganze Stunde her gemacht und haben keine Lösung gefunden bzw. es gibt ja keine

 

[Scorb]

Wenn man es auch einen Baltt Patier versucht ist es NICHT möglich

Ich und 15 andere Leute + Lehrer haben uns über dieses Rätsel ein ganze Stunde her gemacht und haben keine Lösung gefunden bzw. es gibt ja keine

Upps, verschrieben: meinte 4.dimension!

(sollte spass sein)

 

[Krebsnebelwesen]

Upps, verschrieben: meinte 4.dimension!

Auf einem Blatt Papier ist es 2dimensional.

Im Raum ist es 3dimensional. Dort könnte es funktionieren. Habe es nicht nachgebaut

Und die 4. Dimension ist die Zeit. Die wird Dir dabei wohl kaum helfen.
Also mach es nicht schlimmer, als es schon ist...

Im 2dimensionalen ist es nicht möglich, alle Häuser mit allen Werken zu verbinden.

 

[th3o]

warum sollte es in der realität (also 3d) denn funktionieren und 2d nicht? auch in 3d ergeben sich keine neuen wege. er kann nachwievor nur jede brücke einmal benutzen, da wird sich ob 2d oder 3d nichts dran ändern. und es wird sich auch nichts dran ändern dass man immer nur maximal 6 brücken ablaufen kann und eine immer ohne begehung bleiben wird

 

[IRID1UM]

th3o: doch, in der realität könnte man theoretisch um das gewässer herum gehen und somit jede brücke nur ein mal betreten. siehe skizze.
mfg
IRID1UM

 

[Loopo]

Und wenn die 2 grünen Länder Inseln sind!?

 

[Krebsnebelwesen]

warum sollte es in der realität (also 3d) denn funktionieren und 2d nicht? auch in 3d ergeben sich keine neuen wege. er kann nachwievor nur jede brücke einmal benutzen, da wird sich ob 2d oder 3d nichts dran ändern. und es wird sich auch nichts dran ändern dass man immer nur maximal 6 brücken ablaufen kann und eine immer ohne begehung bleiben wird

Äh... Kleines Missverständnis, th3o, ich bezog mich auf das Problem der drei Versorgungswerke und der drei Häuser.

Mit dem Brückenproblem selbst hatte ich mich noch nicht beschäftigt...

 

[th3o]

th3o: doch, in der realität könnte man theoretisch um das gewässer herum gehen und somit jede brücke nur ein mal betreten. siehe skizze.
mfg
IRID1UM

der war gut
in der realität alleine... erstens wäre es erstmal ziemlich doof 2 brücken mit 7 übergängen nur ein paar hundert meter neben dem wasser-ende zu bauen. zweitens steht das problem aber nun mal so dass das wasser auf unbestimmte zeit nicht umgangen werden kann. was auch eher realistisch ist damit brücken ja erst benötigt werden du kannst ja auch nicht sagen: "ich gehe einmal um den nil, dann kann ich die brücke xy von beiden seiten begehen

@intruder
stimmt, sorry