[Sammelthread] Kleine Denksportaufgabe
- Ersteller TeddyBiker
- Erstellt am
Deine Rechnung ist falsch. Es sind nicht nur 25+25 bzw. 24+26 kleine Quadrate, sondern 25x25 bzw. 24x26 kleine Quadrate. Denk' nochmal drüber nach.
Ups, ich sehe gerade, daß du die Seitenlängen meinst. Von den Seitenlängen bzw. dem Umfang kannst du leider nicht auf den Flächeninhalt schließen.
Der Verfasser des Rätsels will zeigen, daß durch Zerlegung des großen Quadrates in drei Dreiecke und einer anderen Zusammensetzung ein anderer Flächeninhalt entstehen kann. Das ist aber nicht möglich. Die Lösung liegt, wie gesagt, darin, daß das die blauen Dreiecke nicht gleich groß sind. Das zweite blaue Dreieck ist größer und das entstandene Rechteck hat auch die Maße 24x26,irgendwas. Somit ist der Flächeninhalt des Rechtecks größer, als der des Quadrates.
Ups, ich sehe gerade, daß du die Seitenlängen meinst. Von den Seitenlängen bzw. dem Umfang kannst du leider nicht auf den Flächeninhalt schließen.
Der Verfasser des Rätsels will zeigen, daß durch Zerlegung des großen Quadrates in drei Dreiecke und einer anderen Zusammensetzung ein anderer Flächeninhalt entstehen kann. Das ist aber nicht möglich. Die Lösung liegt, wie gesagt, darin, daß das die blauen Dreiecke nicht gleich groß sind. Das zweite blaue Dreieck ist größer und das entstandene Rechteck hat auch die Maße 24x26,irgendwas. Somit ist der Flächeninhalt des Rechtecks größer, als der des Quadrates.
Zuletzt bearbeitet:
Tiu
Rear Admiral
- Registriert
- Sep. 2001
- Beiträge
- 5.568
Das Blaue-Dreieck ist in beiden Bildern gleich! Es ist jeweils die Hälfte eines kleines Quadrates. Auch der "Abschnitt" am roten Dreieck ist die Hälfte eines kleinen Quadrates. Nur 25x25 gibt etwas anderes als 24x26! Verkürzt man hier die eine Seitenlänge um ein Quadrat und gibt dieses Quadrat der anderen Seitenlängen hinzu, so erhält man lediglich andere Multiplikatoren!
- Registriert
- Juli 2002
- Beiträge
- 2.124
Ganz einfach: Der rote Flächeninhalt hat sich geändert!
Vorher war die Figur ein Quadrat mit Seitenlänge x. Danach ein Quader mit den Seitenlängen x-1 und x+1. Da jedoch die grüne Fläche nur verschoben wurde, muß die Änderung im roten Flächeninhalt stattgefunden haben.
Mathematisch:
Fg,v := Flächeninhalt grüne Fläche vorher
Fg,n := Flächeninhalt grüne Fläche nachher
Fr,v := Flächeninhalt rote Fläche vorher
Fr,n := Flächeninhalt rote Fläche nachher
Fg,v=x * (x-1) *1/2 = 1/2 * (x²-x)
Fg,n=1/2 * (x-1) * x = 1/2 * (x²-x)
=> Fg,n=Fg,v
Fr,v= x * x - Fg,v = 1/2 (x²+x)
Fr,n= (x-1) * (x+1) - Fg,n = x²-1 - 1/2 * (x²-x) = 1/2 * x² + 1/2 * x -1 =1/2 (x²+) - 1.
Daher kommt also der fehlende Flächenanteil.
CU Endurance
Vorher war die Figur ein Quadrat mit Seitenlänge x. Danach ein Quader mit den Seitenlängen x-1 und x+1. Da jedoch die grüne Fläche nur verschoben wurde, muß die Änderung im roten Flächeninhalt stattgefunden haben.
Mathematisch:
Fg,v := Flächeninhalt grüne Fläche vorher
Fg,n := Flächeninhalt grüne Fläche nachher
Fr,v := Flächeninhalt rote Fläche vorher
Fr,n := Flächeninhalt rote Fläche nachher
Fg,v=x * (x-1) *1/2 = 1/2 * (x²-x)
Fg,n=1/2 * (x-1) * x = 1/2 * (x²-x)
=> Fg,n=Fg,v
Fr,v= x * x - Fg,v = 1/2 (x²+x)
Fr,n= (x-1) * (x+1) - Fg,n = x²-1 - 1/2 * (x²-x) = 1/2 * x² + 1/2 * x -1 =1/2 (x²+) - 1.
Daher kommt also der fehlende Flächenanteil.
CU Endurance
Pfeifenheini
Cadet 4th Year
- Registriert
- Mai 2002
- Beiträge
- 122
Da hast du wohl das rote zusammen mit dem blauen Dreieck gemeint, oder ? Vom Quadrat mit Kantenlänge x einfach das grüne Dreieck abziehen [Fr,v = x * x - Fg,v] ergibt NICHT das rote, sondern den Flächeninhalt des roten zusammen mit dem kleinen blauen Dreieck.
GraKa0815 liegt auch falsch, es ist eben kein 45-Grad-Winkel in irgendeinem der Dreiecke - der Versatz um eine Längeneinheit verhindert dies...
Ansonsten ein kleiner Hinweis: es war nicht gemeint, irgendeinen Flächeninhalt zu ändern, die Aufgabe soll mit Papier und Schere lösbar sein! Deshalb: vielleicht ist ja das neue Rechteck gar nicht genau 24×26 Felder groß, sondern sieht nur so aus
???Die Aufgabe gilt als noch nicht gelöst ...
Zuletzt bearbeitet:
Pfeifenheini
Cadet 4th Year
- Registriert
- Mai 2002
- Beiträge
- 122
No Sir, hat es eben nicht! Wenn du das große Quadrat genau diagonal von Ecke zu Ecke teiltest, hättest du 45 Grad-Winkel. Da aber der (gerade !) Schnitt links unten um ein Feld versetzt beginnt, kann keiner der Winkel bei 45 Grad liegen !
Einen 90 Grad-Winkel hat es allerdings. Wenn du diesen Gedanken konsequent zuende bringst, näherst du dich der Lösung.
@Endurance:
Ich habe eben mal deine Formel nachgerechnet - wenn du davon ausgegangen bist, daß die zweite Fläche tatsächlich 26×24 Felder groß ist, ist deine Lösung richtig. Das war aber, wie gesagt, nicht der Sinn dieser Aufgabe (habe ich vielleicht nicht genau genug formuliert ?). Es sollte ein Quadrat zerschnitten und neu zum Rechteck zusammengesetzt werden, also OHNE Flächenveränderung der einzelnen Bestandteile.
Nach dem "Halb-Lolli-Einkünfteverfahren" würdest du damit aber "halb" anerkannt !
Einen 90 Grad-Winkel hat es allerdings. Wenn du diesen Gedanken konsequent zuende bringst, näherst du dich der Lösung.
@Endurance:
Ich habe eben mal deine Formel nachgerechnet - wenn du davon ausgegangen bist, daß die zweite Fläche tatsächlich 26×24 Felder groß ist, ist deine Lösung richtig. Das war aber, wie gesagt, nicht der Sinn dieser Aufgabe (habe ich vielleicht nicht genau genug formuliert ?). Es sollte ein Quadrat zerschnitten und neu zum Rechteck zusammengesetzt werden, also OHNE Flächenveränderung der einzelnen Bestandteile.
Nach dem "Halb-Lolli-Einkünfteverfahren" würdest du damit aber "halb" anerkannt !
Zuletzt bearbeitet:
Pfeifenheini
Cadet 4th Year
- Registriert
- Mai 2002
- Beiträge
- 122
Na, was biste denn um 17:50 Uhr im Halbschlaf...?
DIE AUFGABE IST IMMER NOCH NICHT GELÖST !
DIE AUFGABE IST IMMER NOCH NICHT GELÖST !
Zuletzt bearbeitet:
BOZ_er
Lt. Commander
- Registriert
- Apr. 2003
- Beiträge
- 1.212
Wenn das Blaue 3eck aber genau die Breite 1 hat und man das ausschneidet und das Rote 3Ecke um 1LE nach rechts schiebt dann sind die Ausmaße des Rechtecks ~26,041*24 = 625
Weil der schnitt nicht ganz 45° ist ist das blaue 3eck höher als breit, man verschiebt auch das rote somit nicht 45°.
Weil der schnitt nicht ganz 45° ist ist das blaue 3eck höher als breit, man verschiebt auch das rote somit nicht 45°.
Pfeifenheini
Cadet 4th Year
- Registriert
- Mai 2002
- Beiträge
- 122
Lolli !
So ist es - das kleine blaue Dreieck und das grüne Dreieck sind ähnliche Dreiecke: beide haben einen rechten Winkel und dieselbe Steigung in der Diagonalen (und damit dieselben Winkel in ihren jeweils entgegengesetzten Ecken). Anders gesagt: wenn man das blaue Dreieck um 180 Grad dreht und "aufbläst", wird es deckungsgleich mit dem Grünen !
Da das grüne Dreieck 24 Felder breit und 25 Felder hoch ist, muß dann das blaue Dreieck (bei Breite 1 Feld) die Höhe 25/24 Felder [= 1 1/24] haben.
Diese Höhe addiert sich im rechten Bild zur Höhe des roten Dreiecks (25 Felder). Das neu entstandene Rechteck auf dem rechten Bild ist also in Wirklichkeit 24 Felder breit und 26 1/24 [= 625/24] Felder hoch - Rauminhalt = 625/24 × 24 = 625. So leicht kann man sich optisch täuschen lassen...
So ist es - das kleine blaue Dreieck und das grüne Dreieck sind ähnliche Dreiecke: beide haben einen rechten Winkel und dieselbe Steigung in der Diagonalen (und damit dieselben Winkel in ihren jeweils entgegengesetzten Ecken). Anders gesagt: wenn man das blaue Dreieck um 180 Grad dreht und "aufbläst", wird es deckungsgleich mit dem Grünen !
Da das grüne Dreieck 24 Felder breit und 25 Felder hoch ist, muß dann das blaue Dreieck (bei Breite 1 Feld) die Höhe 25/24 Felder [= 1 1/24] haben.
Diese Höhe addiert sich im rechten Bild zur Höhe des roten Dreiecks (25 Felder). Das neu entstandene Rechteck auf dem rechten Bild ist also in Wirklichkeit 24 Felder breit und 26 1/24 [= 625/24] Felder hoch - Rauminhalt = 625/24 × 24 = 625. So leicht kann man sich optisch täuschen lassen...
10tacle
Admiral
- Registriert
- Juni 2003
- Beiträge
- 8.918
Eine Quest für clevere!!
Ein Freund hat mir eben eine knifflige frage gestellt und ich komm einfach nicht auf die Lösung. Vieleicht hab ich den Kopf nicht frei für sowas aber ich will euch das nicht vor enthalten. Also hier die Quest:
Du bist in einem Raum mit zwei Türen. An jeder der beiden Türen steht ein Wächter. Ein Tür führt in die Freiheit die andere Tür in den Tod. Du hast eine Frage die du den Wächtern stellen kannst um die richtige Tür zu finden, allerdings einer der beiden sagt die Wahrheit und der andere lügt. Du hast aber keine Ahnung wer jetzt wo steht.
Was muss man nun die Wächter fragen um die richitge Tür zu erwischen???
Ein Freund hat mir eben eine knifflige frage gestellt und ich komm einfach nicht auf die Lösung. Vieleicht hab ich den Kopf nicht frei für sowas aber ich will euch das nicht vor enthalten. Also hier die Quest:
Du bist in einem Raum mit zwei Türen. An jeder der beiden Türen steht ein Wächter. Ein Tür führt in die Freiheit die andere Tür in den Tod. Du hast eine Frage die du den Wächtern stellen kannst um die richtige Tür zu finden, allerdings einer der beiden sagt die Wahrheit und der andere lügt. Du hast aber keine Ahnung wer jetzt wo steht.
Was muss man nun die Wächter fragen um die richitge Tür zu erwischen???
M.o.D
Lt. Commander
- Registriert
- Nov. 2002
- Beiträge
- 1.234
Sorry, dass ich mich so unverständlich ausgedrückt habe. Ich habe es so geschrieben, wie es mir als erstes eingefallen ist.
Und wenn ihr damit meint ich wäre dumm und könne keine anständigen Sätze formulieren, dann muss ich euch entäuschen. Ich besuche ein Gymnasium und hab gute Noten. Aber ich wusste nicht, dass man hier im Forum, ganz besonders im "FunStuff", auf Grammatik und Rechtschreibung achten muss. Aber wenn ich sehe, dass dies ein paar Boardies stört, so werde ich mich in nächster Zeit bemühen ordentliche Sätze zu posten.
Mit freundlichen Grüßen
euer Meister des Disasters(Master of Disaster)
Und wenn ihr damit meint ich wäre dumm und könne keine anständigen Sätze formulieren, dann muss ich euch entäuschen. Ich besuche ein Gymnasium und hab gute Noten. Aber ich wusste nicht, dass man hier im Forum, ganz besonders im "FunStuff", auf Grammatik und Rechtschreibung achten muss. Aber wenn ich sehe, dass dies ein paar Boardies stört, so werde ich mich in nächster Zeit bemühen ordentliche Sätze zu posten.
Mit freundlichen Grüßen
euer Meister des Disasters(Master of Disaster)
10tacle
Admiral
- Registriert
- Juni 2003
- Beiträge
- 8.918
Keiner erwartet ne perfekte Formulierung ohne Rechtschreibfehler und perfekter Grammatik. Aber bei deinem Satz war es halt wirklich sehr schwer zu verstehen. Aber immerhin hast du das Rätsel vor mir gelöst!!!
So hier noch ne Denkaufgabe:
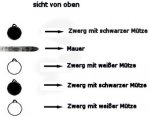
Ein Riese gräbt 4 Löcher im Boden. In die er 4 Zwerge bis zum hals einbuddelt. Jeder der Zwerge hat eine Mütze auf. Keiner weiß jedoch die Farbe der Mütze. Der Riese beschließt den Zwerg frei zu lassen, der die Farbe seiner Mütze herausfindet. Sie können nur eine Antwort geben. Ist sie falsch, müssen alle sofort Sterben. In den Löschern sitzen sie hintereinander, schauen alle in eine Richtung (auf dem Bild nach oben) und dürfen sich nicht umdrehen und nichts untereinander reden. Zwischen dem letzten und vorletztem ist sogar noch eine Mauer über die man nicht drüber schauen kann.
Die Zwerge bekommen nur die Information, dass es 2 weiße und 2 schwarze Mützen gibt.
Wer von den 4 Zwergen kommt durch die richtige Antwort frei?
Anhänge
Zuletzt bearbeitet: