[Sammelthread] Kleine Denksportaufgabe

[Timbo]

Sag mal Curt, hast du dir das Rätsel eigentlich durchgelesen?

 

[tobytobsucht]

Sieht nicht so aus!

 

[kurt cobain]

Sorry, aber wieso die Frage? Das mit dem Tag steht nicht drin, ist eine Annahme. Und es muss ja nicht unbedingt was mit dem Schalter zu tun haben, bzw es gibt solche Rätsel.

 

[Tiguar]

Frage @toby: Wird denn aus den 23 die komplette Reihenfolge ausgelost, und dann gehen die Knackis in der gelosten Reihenfolge in den Raum, oder wird immer einer aus den vollen 23 ausgewählt?

Für den ersten Fall hätte ich die Lösung!

Ciao, Tiguar

 

[tobytobsucht]

Der Direktor nimmt sich immer ganz zufällig einen Gefangen aus den 23 herraus und schickt ihn in den Raum d.h. die Reihenfolge ist nicht vorher bestimmt.

Es kann also theoretisch sein, dass ein Gefangener erst nach 10 Monaten das erste mal in den Raum kommt, oder aber das ein anderer Gefangener 10mal nacheinander in den Raum geschickt wird. (deshalb habe ich auch geschrieben, dass es mit der richtigen Lösung trotzdem lange dauern kann bis alle freikommen)


Aber schreib doch mal Deine Lösung für den anderen Fall. Vielleicht ergibt sich daraus ja was!

 

[Tiguar]

Na ja, so toll ist die Lösung nicht, denn im ersten Fall wüßte jeder Gefangene, der zum zweiten Mal in den Raum kommt, daß dann alle anderen vor ihm schon mindestens einmal dringewesen sein müssen. Wäre ja auch zu einfach, man bräuchte die Schalter wieder nicht, daher sorry für den Schnellschuß!

Eine andere Überlegung geht dahin, daß einer ausgewählt wird, nur den einen Schalter zu betätigen, während alle anderen sich an dem anderen austoben. Bringt aber irgendwie auch nichts ....

Hast Du nicht noch eine kleine Hilfe, sonst werde ich hier echt noch zum Elch ...

CU, Tiguar

 

[Endurance]

Also, die Häftlinge einigen sich auf einen Mann A der einen vorher bestimmten Schalter in eine vorher ausgemachte Position bringt. Sollte anderer Häftling den Raum betreten und dieser Schalter (als Beispiel mal der von der Tür links gesehene) in der vorbestimmten Position sein, ändert der Häftling B-Z eben diesen vorbestimmten linken Schalter in die andere Position. Ist dieser noch nicht oder schon wieder in der nicht ausgemachten Position, so darf er nur den anderen (hier halt den rechts von der Tür gesehenen) betätigen. Nur Häftling A darf den linken Schalter wieder zurücksetzen. Wenn Häftling A diesen vorher ausgemachten Schalter dann zum 23. Mal zurückgesetzt hat, das erste Mal muß er ihn ja in die vorbestimmte Position bringen, kann er dem Direktor mit 100%-tiger Sicherheit sagen, dass alle mindestens einmal in dem Raum gewesen sind.

Und alles verstanden?

 

[Tiguar]

Original erstellt von Endurance
Und alles verstanden?

Nö! Häftling A weiß dann nur sicher, daß ein anderer 23 Mal in dem Raum gewesen sein muß. Das kann dann aber auch 23 Mal Häftling B gewesen sein. Letztlich kann A so nur feststellen, ob er zweimal nacheinander in den Raum gekommen ist, ohne daß ein anderer in der Zwischenzeit drin war.

Für eine 100%-ige Sicherheit reicht das imho nicht.

Ciao, Tiguar

 

[Endurance]

Hatte vergessen zu erwähnen, dass Häftlinge B-Z nur einmal den Schalter auf der linken seite umlegen dürfen. Aber halt auch nur dann, wenn der vorher in der festgelegten position war.

 

[Tiguar]

Okay, dann scheint es zu passen.

Greetz, Tiguar

 

[[DZF]_ARES]

nicht wenn Häftling A nicht bis 23 zählen kann

 

[tobytobsucht]

@ endurance


Glückwunsch!! Lösung ist richtig!

Bist Du selber drauf gekommen oder hasse irgendwo nachgeschaut?!


Ich such gleich mal das nächste Rätsel,

aber erstmal....

 

[Timbo]

Verdammt! Das geht ja wirklich. Nicht schlecht, Herr Specht.

 

[[DZF]_ARES]

Nein. Das ist noch nicht ganz des Rätzels Lösung. Was wäre den, wenn Häftling A zufällig als erster in den Raum kommt, und den Schalter in der Position sieht die die Häftlinge als Zeichen ausgemacht haben.
Dann weiß er ja nicht, ob er der Erste ist oder ob jemand vor ihm den Schalter schon betätigt hat.
Geht er dafon aus, dass er der erste ist, und es stimmt nicht, dann wartet er auf das 23 mal bis er schwarz wird.
Geht er davon aus, das er nicht der erste is, so wird er schon beim 22 mal dem Direktor sagen das alle Häftlinge im Raum waren und alle sitzen bis an das Ende ihrer Tage.

Richtig ist : Jeder Gefangene mus den ausgemachten Schalter 2 mal betätigen. Erst beim 45. mal kann Häftling A genau sagen das alle mindestens einmal im Raum waren.

 

[Endurance]

@tobytobsucht: bin selbst draufgekommen. HAb heute in der arbeit aber die Lücke, die auch [DZF]_ARES erwähnt hat erkannt und bin zu gleicher Schlußfolgerung gekommen. Also Congrats [DZF]_ARES

Nur so ergänzend: Es kann auch einer der anderen Häftlinge sagen, wann schluß ist, wenn er immer mitzählt und zufällig immer nach dem rücksetzen durch A reinkommt und sieht, dass der Schalter 45-mal "vorgestellt" wurde .

 

[tobytobsucht]

Das mit dem 45sten mal ist natürlich richtig! Es ist sogar die einzige richtige Lösung, egal ob A nun als erster, zweiter oder sonstwas in den Raum kommt. Wenn er das erste mal den Schalter umlegt, weiss er nie ob schon jemand im Raum war.

Aber ich denke Du darfst den Lollie trotzdem behalten, Endurance! Schließlich hast Du das Rätsel ja so gut wie gelöst.

An [DZF]_ARES geht natürlich auch ein Lollie!!


So...jetzt seit Ihr wieder dran...ich will auch mal wieder rätseln.

 

[Endurance]

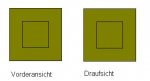
Ein Meister gibt seinem Tischlerlehrling die folgende Skizze (siehe Anhang)
und fordert ihn auf, den dargestellten Körper herzustellen.
Völlig verzweifelt zeigt der Lehrling die Skizze seinem Freund,
da er der Meinung ist, daß ihn der Meister reinlegen will.
Doch der Freund zeichnet ihm den Körper in der Schrägansicht auf
und hilft damit dem Lehrling aus der Klemme.

Wie muss der Körper aussehen?

(Hinweis: Es gibt keine verdeckten Linien, sonst wären sie dargestellt.)

 

[Bombwurzel]

Nunja, es müssen wohl quadratische Vertiefungen in den Würfel eingelassen werden.

Steht blos die Frage, wie tief die sein müssen...

 

[kunakuna]

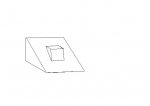
Habe hier eine Lösung zur Tischlehrling Aufgabe.
Sollte stimmen.

Ich habe noch ein neues Rätsel. Ich habe die Lösung (leider) nur durch ausprobieren herausgefunden. . Aber vielleicht kann mir ja jemand helfen, den Lösungsweg herauszufinden.

Hier das Polizeirätsel:
Eine Gruppe von Polizisten muss eine unbekannte Anzahl Gefangene vom Gerichtshof zu den Gefängnissen begleiten. Es stehen 2 Busse mit je 50 Plätzen zur verfügung. (Max 100 Plätze)

Beim ersten Halt steigt ein Drittel der Mitreisenden (Polizisten und Gefangene) aus und 2 Polizisten steigen ein. Die Gesamtanzahl wird kleiner.

Beim zweiten Halt steigt wieder ein Drittel der Mitreisenden aus und zwei Polizisten kommen dazu.

Beim dritten Halt steigt wieder ein Drittel der Mitreisenden aus und zwei Polizisten kommen dazu.

Beim vierten Halt steigt wieder ein Drittel der Mitreisenden aus und zwei Polizisten kommen dazu. Jetzt sollten nur noch Polizisten übrig sein.
Wie viele Polizisten bleiben übrig?
Viel Spass

 

[PuppetMaster]

Verdammt! Habs gewusst, nur zu lange zum konstruieren gebraucht.

Hier noch meine Lösung, wens interessiert...