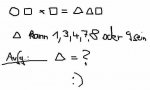[Sammelthread] Kleine Denksportaufgabe
- Ersteller TeddyBiker
- Erstellt am
das fehlende Quadrat
Warscheinlich kennt ihr das schon aber, aber kann mir einer mal erklären,warum das so ist?
Ich habs mir schon oft angeguckt und das ganze Dreieck hat eine Fläche von 32,5 cm² (wenn man ein Kästchen als 1 cm nimmt), die gesamte Fläche der einzelnen Komponenten ist 32 cm². Ich weis es nicht genau, aber kann es sein, dass die Hypotinose oben zu rechten Winkel hin und unten von dem selbigen weg gebogen ist?
cju
Warscheinlich kennt ihr das schon aber, aber kann mir einer mal erklären,warum das so ist?
Ich habs mir schon oft angeguckt und das ganze Dreieck hat eine Fläche von 32,5 cm² (wenn man ein Kästchen als 1 cm nimmt), die gesamte Fläche der einzelnen Komponenten ist 32 cm². Ich weis es nicht genau, aber kann es sein, dass die Hypotinose oben zu rechten Winkel hin und unten von dem selbigen weg gebogen ist?
cju
Zuletzt bearbeitet:
deltafox
Hardcore Member
- Registriert
- Apr. 2001
- Beiträge
- 1.403
@kunakuna
Das mit der Anfangszahl von 87 Personen scheint zustimmen.
Wenn ich das mal durchrechne:
87
- 29 erster Halt: - ein drittel
= 58
+ 2 zusteiger
= 60
- 20 zweiter Halt: - ein weiteres drittel
= 40
+ 2 zusteiger
= 42
- 14 dritter Halt: - nochmal ein drittel
= 28
+ 2 zusteiger
= 30
- 10 vierter Halt: das letzte drittel
= 20
+ 2 zusteiger
= 22 Bullizisten
Hast recht.
Kommt wahrscheinlich dadurch zustande, das nur bei 87 als Anfangszahl - ein drittel +2 ; immer wieder eine durch 3 teilbare Zahl herraus kommt.
Das mit der Anfangszahl von 87 Personen scheint zustimmen.
Wenn ich das mal durchrechne:
87
- 29 erster Halt: - ein drittel
= 58
+ 2 zusteiger
= 60
- 20 zweiter Halt: - ein weiteres drittel
= 40
+ 2 zusteiger
= 42
- 14 dritter Halt: - nochmal ein drittel
= 28
+ 2 zusteiger
= 30
- 10 vierter Halt: das letzte drittel
= 20
+ 2 zusteiger
= 22 Bullizisten
Hast recht.
Kommt wahrscheinlich dadurch zustande, das nur bei 87 als Anfangszahl - ein drittel +2 ; immer wieder eine durch 3 teilbare Zahl herraus kommt.
tobytobsucht
Ensign
- Registriert
- Juli 2001
- Beiträge
- 219
30 mal???
durch 7 teilbar: 0-70 = 10 mal; 71-133 = 9 mal ----> 19 mal
Endung auf 7: (7), 17, 27, 37, 47, 57, 67, (77), 87, 97, 107, 117, 127 --->11 mal, da bei 7 und 77 nur einmal geklatscht wird!
Richtig? Oder hab ich was übersehen??
durch 7 teilbar: 0-70 = 10 mal; 71-133 = 9 mal ----> 19 mal
Endung auf 7: (7), 17, 27, 37, 47, 57, 67, (77), 87, 97, 107, 117, 127 --->11 mal, da bei 7 und 77 nur einmal geklatscht wird!
Richtig? Oder hab ich was übersehen??
tobytobsucht
Ensign
- Registriert
- Juli 2001
- Beiträge
- 219
Dann mach ich nochmal eins (wir hatten hier schonmal ein ähnliches, aber das hier ist etwas erweitert):
Du kommst an eine Weggabelung und weißt nicht, ob der linke oder der rechte Weg zu Deinem Ziel führt. Glücklicherweise ist gleich in der Nähe ein Haus, deren Bewohner Du fragen kannst.
In dem Haus wohnen drei Brüder. Einer sagt immer die Wahrheit, einer lügt immer, und der dritte lügt manchmal und manchmal nicht. Du weißt aber nicht, wer der drei Brüder wer ist.
Du darfst zwei beliebige Fragen stellen, um herauszufinden, wohin du gehen mußt, um Dein Ziel zu erreichen.
Was mußt du wen fragen?
Du kommst an eine Weggabelung und weißt nicht, ob der linke oder der rechte Weg zu Deinem Ziel führt. Glücklicherweise ist gleich in der Nähe ein Haus, deren Bewohner Du fragen kannst.
In dem Haus wohnen drei Brüder. Einer sagt immer die Wahrheit, einer lügt immer, und der dritte lügt manchmal und manchmal nicht. Du weißt aber nicht, wer der drei Brüder wer ist.
Du darfst zwei beliebige Fragen stellen, um herauszufinden, wohin du gehen mußt, um Dein Ziel zu erreichen.
Was mußt du wen fragen?
Timbo
Lieutenant
- Registriert
- Juli 2001
- Beiträge
- 713
Meines Erachtens reicht da sogar nur eine Frage. Sagen wir mal die drei stehen in einer Reihe. Nennen wir sie einfach 1, 2 und 3. So, jetzt frage ich nummer 1:
"Was sagt dir nummer 2, wenn er nummer 3 nach dem richtigen weg fragen würde." Die brüder sind zwar teilweise Lügner, aber nicht blöd. deshalb denkt er kurz nach und sagt dir den richtigen weg. Warum? ganz einfach.
nehmen wir an 1 und 2 sind Lügner. 3 sagt die wahrheit. dann würde 3 die wahheit sagen, 2 macht daraus eine Lüge und 1 wieder die wahrheit.
auch wenn die drei in einer anderen reihenfolge rumstehen kommt das selbe heraus. 2 lügt, 3 wiederholt die Lüge und 1 macht die wahrheit raus. Ganz einfach.
-Timbo
"Was sagt dir nummer 2, wenn er nummer 3 nach dem richtigen weg fragen würde." Die brüder sind zwar teilweise Lügner, aber nicht blöd. deshalb denkt er kurz nach und sagt dir den richtigen weg. Warum? ganz einfach.
nehmen wir an 1 und 2 sind Lügner. 3 sagt die wahrheit. dann würde 3 die wahheit sagen, 2 macht daraus eine Lüge und 1 wieder die wahrheit.
auch wenn die drei in einer anderen reihenfolge rumstehen kommt das selbe heraus. 2 lügt, 3 wiederholt die Lüge und 1 macht die wahrheit raus. Ganz einfach.
-Timbo
tobytobsucht
Ensign
- Registriert
- Juli 2001
- Beiträge
- 219
@timbo
Wenn aber jetzt der "Unentschlossene" die Wahrheit sagt, dann funktioniert das ganze nicht mehr. Man weiss ja nicht, ob dieser eine gerade lügt oder nicht.
Also...
ne andere Lösung muss her!
Wenn aber jetzt der "Unentschlossene" die Wahrheit sagt, dann funktioniert das ganze nicht mehr. Man weiss ja nicht, ob dieser eine gerade lügt oder nicht.
Also...
ne andere Lösung muss her!
