16bit in 2*8bit umwandeln

[Krik]

Also sind die CPUs (noch) nicht in der Lage, eine Reihe von unterschiedlichen sequentiell ablaufende Befehle in einem Takt abzuarbeiten. Bei parallelisierbaren Befehlen, deren Ergebnisse nicht voneinander abhängen, ist es hingegen möglich. Ist das so korrekt?

 

[maxwell-cs]

man kann in jedem deterministischem programm, das eine der beiden zeilen enthält, sie durch die andere ersetzen und das programm wird das gleiche tun (bis eben auf den effizienzunterschied).

für mich erfüllt das die eigenschaft "gleiches verhalten".

edit: dieser post war auf die mittlerweile wegeditierte antwort bezogen.

 

[ice-breaker]

@e-Laurin: Ja, aber es wird auch nie möglich sein, mehrere sequentielle Befehlte immer gleichzeitig auszuführen.

a = b + c
a = a * a

Hier hängt nunmal der 2. Befehl vom ersten ab, kann also nicht gleichzeitig ausgeführt werden. Ob generell konfliktfreie sequentielle Befehle parallel ausgeführt werden, weiß ich nicht, da kenne ich die aktuelle x86-Architektur zu wenig. Man ist aber vor Jahren sowieso von dem Weg weggegenangen eine Operation in einem Takt auszuführen, worauf du dich so einschiest. Denn dann würde jeder Takt so lange brauchen, wie die langsamste Operation. Aus dem Grund wird jede Operation in mehreren Takten ausgeführt, so ist jede Operation so schnell wie sie sein kann. Und langsame Operationen führen nicht dazu, dass schnelle Operationen auch langsam werden müssen, damit 1 Befehl immer genau in 1 Takt ausgeführt wird.


@maxwell-cs: sind identisch, hatte es nur nicht schnell genug wieder wegeditiert *gg*

 

[Krik]

Man ist aber vor Jahren sowieso von dem Weg weggegenangen eine Operation in einem Takt auszuführen, worauf du dich so einschiest. Denn dann würde jeder Takt so lange brauchen, wie die langsamste Operation. Aus dem Grund wird jede Operation in mehreren Takten ausgeführt, so ist jede Operation so schnell wie sie sein kann. Und langsame Operationen führen nicht dazu, dass schnelle Operationen auch langsam werden müssen, damit 1 Befehl immer genau in 1 Takt ausgeführt wird.

Ehrlich gesagt, ich habe nicht verstanden, was du hier ausdrücken willst. Vielleicht bin ich gerade doof, keine Ahnung.

Es ist doch schneller, wenn eine CPU in einem Takt mehrere Befehle ausführen kann (und es wäre noch schneller, wenn die Ergebnisse dieser Befehle auch voneinander abhängen dürfen - ob das aktuell möglich ist, weiß ich nicht). Du sagst jetzt, es wäre schneller, wenn eine CPU x Takte für einen Befehl benötigt. Irgendwie kann ich nicht nachvollziehen, was du ausdrücken möchtest.

 

[maxwell-cs]

er meint: wenn man sich nicht darauf festlegt, dass jeder befehl nur einen takt benötigen darf, kann man einzelne takte entsprechend schnell machen, sodass kurze befehle immer noch nur einen (aber jetzt kürzeren!) takt brauchen, während komplexere befehle mehrere takte brauchen, die aber genauso lange dauern wie sonst ein takt.

 

[Krik]

Ok, jetzt bin ich baff. Du hast es gerafft und ich nicht. ^^

Was meinst du mit kürzeren Takt? Die Takte dauern doch alle gleich lang.
Dann sagst du noch, dass komplexe Befehle mehrere Takte brauchen, aber nur einen Takt dauern. Das widerspricht sich doch.

Ich muss da irgendwo eine Denkblockade haben.
Kann mir vielleicht jemand ein konkretes Beispiel (mit aus der Luft gegriffenen Werten) geben?

 

[ice-breaker]

Also eine Operation besteht vereinfacht aus folgenden Phasen: nächste Instruktion laden, Instruktion decodieren und Daten laden, Ausführen, Ergebnisse zurückschreiben

Die sehr frühen CPU-Architekturen haben gesagt, dass diese ganzen Phasen zusammen ein Block sind. Sie finden in einem einzelnen Takt statt. Das Problem dabei ist aber doch, dass das Ausführen unterschiedlich lange benötigt. Eine Bitweise Negierung ist ziemlich einfach, da kann jedes Bit parallel negiert werden. Ist also extrem schnell. Eine Addition hingegen (man denke an Halb- und Volladdierer) besteht aus vielen Operationen, die nacheinander ausgeführt werden müssen. Warum sollte also nun die Negierung genauso langsam wie die Addition sein? Nur damit alles in einem Takt passiert?
Und aus dem Grund ging man weg von Architekturen bei denen ein Befehl in einem Takt ausgeführt wird und baute Architekturen bei denen die Negierung eben 3 Takte benötigte, und die Addition 7 Takte. Nur dass alles nun 7 mal so schnell ausgeführt wird. Die Addition ist nicht schneller geworden, denn alles wird zwar 7mal so schnell ausgeführt aber die Operation benötigt nun auch 7 Takte. Aber die Negierung arbeitet nun schneller, da nur noch 3 der neuen 7mal schnelleren Takte benötigt werden.
Genauso gibt es den Vorteil, dass schon der nächste Befehl geladen und dekodiert werden kann, während der vorherige noch bearbeitet wird. Also wieder schneller.

Was vorher einfach eine lange Aktion war wurde in mehrere kleine Schritte aufgeteilt, die jede für sich schneller abläuft. Dafür sind nun aber mehrere Schritte nötig. Und es können Teile parallel abgearbeitet werden. So kann z.B. schon die nächste Instruktion geladen werden, während die Instruktion davor noch berechnet wird. Aber auch nur Teile, die wie in #23 beschrieben sich nicht überschneiden und zu einem falschen Ergebnis führen würden. Für das Problem in #23 müsste eben für die Ausführung von Operation 2 auf das Ergebnis von Operation 1 gewartet werden, der Prozessor würde also einige Takte nichts machen. Und genau an dieser Stelle kommt von Intel das Hyperthreading ins Spiel: Statt nichts zu tun, kann eine Operation eines anderen Threads ausgeführt werden. Das ist der Grund warum HT z.B. nur 20% schneller ist, weil es nur da eingesetzt werden kann, wo der Prozessor warten müsste. Die mehreren Integer-Operationen der AMD-Architektur sind ein ziemlich ähnliches Modell, aber eine ganze Ecke komplexer: Im Prinzip bestimmt jeder Core in der K10-Architektur welche folgenden Integer-Operationen er alle parallel berechnen kann, ohne dass diese voneinander wie in #23 abhängig sind. Und diese werden dann berechnet.

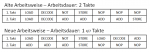
Wikipedia hat ein schönes Beispiel welchen Unterschied die Parallelität der mehreren einzelnen Phasen mit einzelnen Takten gegenüber dem 1 Takt pro Befehl Modell macht: http://de.wikipedia.org/wiki/Pipeline_(Prozessor)

Ist es jetzt verständlicher?

 

[Daaron]

Ist auch ziemlich wirr... denn eigentlich passiert nur genau zum CL-Signal innerhalb einer Schaltung irgend etwas. Manche Sachen sind komplex, die brauchen mehrere Takte. Andere sind extrem einfach, deren Abarbeitung dauert einen Takt. Niemals dauert aber eine komplexe (mehrstufige) Aufgabe nur einen Takt.

 

[ice-breaker]

Meine Erklärung ist wirr oder wie das Taktmodell funktioniert?

Jup, was du beschreibst ist eben die moderne Pipeline einer Mehrtaktimplementierung, aber e-Laurin schien von dem antiquierten Eintaktmodell auszugehen, zumindest kam es so rüber.

 

[Krik]

Ist das so wie im Anhang gemeint? Da ist allerdings nicht berücksichtigt, was er parallel verarbeiten kann. Und es ist auch stark vereinfacht dargestellt.

 

[ice-breaker]

Ja das trifft es.
Im oberen Modell muss eben alles gleichlang dauern (1 Takt pro kompletter Befehl), dadurch werden am ende NOPs (No Operation) eingefügt. Nur dass es eben keine NOPs waren sondern durch die Schaltungen bedingt war.
Beim unteren Beispiel ist aber jeder Schritt eines Befehls nun in einem einzelnen Takt, der n-mal schneller ist. So kann mit der Berechnung der Addition (Befehl 2) früher begonnen werden, da Befehl1 mit dem neuen Modell schneller fertig ist. Aber Befehl 2 ist mit dem neuen Modell trotzdem genauso langsam, wie im alten Modell. Alles läuft nun zwar n-mal schneller, aber die Operation braucht nun eben n-Takte.
Mit Parallelität hat das aber noch nichts zu tun, das Beispiel ist nicht parallel. Wie es parallel funktioniert erklärt dir der verlinkte Wiki-Artikel. Das ist aber eben die Parallelisierung ohne Hyper Threading und ohne die 4 ALU-Operationen im AMD K10-Modell, das wird dann nochmal auf das Modell draufgesetzt.

 

[Krik]

Jut, dann habe ich es jetzt verstanden. Ich kam durcheinander, weil ihr Takt einmal im Sinne von Prozessortakt und einmal im Sinne von Arbeits(teil)schritt verwendet habt. Es war also wie üblich ein Kommunikationsproblem.

 

[Daaron]

Meine Erklärung ist wirr oder wie das Taktmodell funktioniert?

Jup, was du beschreibst ist eben die moderne Pipeline einer Mehrtaktimplementierung, aber e-Laurin schien von dem antiquierten Eintaktmodell auszugehen, zumindest kam es so rüber.

Nä, deine nicht... ich war nur zu lahmarschig beim posten, weil ich grad noch was anderes zu tun hatte...

aber Pipelines (also quasi alles ab den späten neuzigern) sind noch um einiges komplexer. Bei ner Pipeline wird gleichzeitig ein Befehl abgearbeitet, einer dekodiert und einer geholt (bzw. sogar mehrere parallele Bearbeitungsschritte). Dabei darf man es aber nicht übertreiben, sonst wird die Sprungvorhersage zu komplex und die Pipeline ist zu oft mit Müll gefüllt, der wieder verworfen werden muss.
Die Rache von elend langen Pipelines mit zu vielen Stufen hatte man dann beim P4 vs. Athlon XP. Der Athlon XP mit seinen eher kurzen Pipelines und seiner guten Sprungvorhersage war am Ende bei grob 60% des Taktes genau so leistungsstark wie der P4, der sich mit wirklich ellenlangen Pipelines brüsten wollte. Schade eigentlich, dass Intel dazu gelernt haben mit der der Core-Technologie... sonst wäre AMD inzwischen Marktführer.
Und ja: ich hab das Zeug echt noch gelebt. Ich bin so alt. Ich hab sogar schon 286er außerhalb eines Museums in Aktion erlebt... die 30 droht mir bald...

 

[Dshing]

Also bei mir handelt es sich um ein 8Bit AVR Controller (keine Hausaufgabe ^^ ).
Demnach wäre es dann gleich schnell, aber für die Division bräuchte ich doch dann ein doublel, um keinen Fehler beim zerlegen zu bekommen?
Also:

unsigned short s;
unsigned char x2 = s/256;
unsigned char x1 = (s/256-x2)*256;

Würde er dann die letzte Zeile nicht falsch berechnen?

 

[AP Nova]

Ich verstehe ehrlich gesagt nicht wirklich, was du in der letzten Zeile berechnen willst. (Zumal du ja bereits einfache Lösungsvorschläge erhalten hast)
In x2 speicherst du ja anscheinend die 8 höchsten Bits, in x1 willst du dann entsprechend die 8 niedrigen Bits speichern?

x1 = s % 256;

So berechnest du den Rest, der bei einer Division von s mit 256 übrig bleibt (also kommt da 0 bis 255 raus)

 

[ice-breaker]

Ich weiß zwar nicht, was du in deiner letzten Zeile machen willst, aber es ist garantiert falsch. Denn es wird immer 0 herauskommen, da deine Berechnung nach Ersetzung {x2 -> s/256} folgendermaßen lautet:

unsigned char x1 = (s/256-s/256)*256;

und siehe da, der Inhalt der Klammer kann nur Null sein, somit auch x1.

 

[Dshing]

Achso, das Modulo gibt es ja auch noch. Ich hatte jetzt überlegt, wie man mit Division darauf käme, bei gleichem Ressourcen verbrauch. Da bräuchte man eben dann in der zweiten Zeile die Nachkommastellen des Quotienten und das ginge ja nicht ohne Modulo nur mit einem 8bit Zeichen.
Laufen tut das ganze schon mit dem Bitshift, war jetzt nur für mein Verständnis.