XLS Wahrscheinlichkeitsrechnung

[species_0001]

Hallo zusammen,

ich hab da mal ein Problem.
Wahrscheinlichkeitsrechnung.
Asche auf mein Haupt: Ich hatte es zwar im Abi, aber es ist einfach zu lange her und es ist nichts von übrig geblieben. Man wird eben alt und google, ja, ich hab gegoogelt, aber ich verstehe die Beispiele nicht mal mehr
also, mein Randgrößen sind:

Gesamtheit aller Elemente: 8000
Stichprobengröße: 40 (im Moment 40, wird laufend vergrößert)
bei der Stichprobengröße wird auf "richtig" und "falsch" geprüft
man hat festgestellt, dass von der Stichprobe 80% das Ergebnis "falsch" zurück gegeben hat.

gesucht wird die Prognose(?) / die Wahrscheinlichkeit von "falsch" auf die Gesamtgröße

konkreter: die 8000 Elemente sind Zählergebnisse an bestimmten Punkten (also Zahlenwerte 1-100). die wurden vor längerer Zeit erfasst. jetzt hat man an zufällig ausgewählten Punkten das Zählergebnis neu ermittelt (also neue Zahlenwerte 1-100 für die jeweiligen Zählpunkte). Dabei ist es völlig egal wie sehr sich die Zahlen an den einzelnen Punkten unterscheiden, es interessiert nur: Zahlenwert ist noch gleich = "richtig" oder weicht ab = "falsch". Und demjenigen der es jetzt bezahlen müsste alle 8000 Punkte neu auszuzählen, wäre es gut, wenn man jetzt wahrscheinlichkeitsrechnungsfundiert sagen würde "hier hör zu, wenn bei der Stichprobe 80% falsch waren, sind mit einer Wahrscheinlichkeit von xx% die Punkte der Gesamtmenge auch falsch, also wenn du da stimmige Zahlenwerte haben willst, musst du alles neu auszählen"

also in xls übertragen:


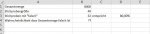
Ich weiß, die Stichprobengröße ist zu klein (aber sie wird ja ständig vergrößert) und man könnte/müsste noch eine Fehlerwahrscheinlichkeit für die Prognose abgeben, aber das wäre optional.


Also wenn da zufällig jemand gerade in der Materie ist und eine Formel für mich hätte, wäre ich sehr dankbar.

 

[BrainFart]

Ich seh das Problem nicht? Wenn die Stichprobe halbwegs repräsentativ ist (gleich viele Proben aus jeder Charge, etc.), und 80% der Stichproben sind "falsch", kann man daraus schließen, dass auch 80% der Gesamtmenge "falsch" ist, das ist der Sinn einer Stichprobe...

 

[blueGod]

@ Brainfart, verstehe Deinen Gedankengang, nur ist das eben keine Wahrscheinlichkeitsrechnung
Nur weil Deine Stichproben zu 80% falsch sind, muss das ja nicht zwangsläufig - auch wenn der Gedanke nahe liegt - auf die Gesamtmenge zutreffen.

@TE Ich hätte auf Anzahl der falschen Stichproben, geteilt durch die Zahl der möglichen Elemente getippt.
Ist aber vermutlich zu einfach, oder?

 

[species_0001]

aber Anzahl falsche Stichproben (32) / 8000 = 0,004 = 0,4% ... ne, das ja so erstmal schlicht der Anteil der falschen Punkte an der Gesamtmenge. eine Aussage über die Gesamtfehlerwahrscheinlichkeit kanns auch noch nicht sein
@Brainfart... ja, das sagt einem der gesunde Menschenverstand, aber es ist zu einfach. Da gibts lustige Formeln zu wie man das ausrechnet, aber ich habe eben überhaupt keine Ahnung mehr, wie das ging.

 

[_killy_]

Du müsstest erst einmal beweisen, dass deine Stichprobe von 40 auch normalverteilt ist. Wenn dies nicht der Fall ist, darfst du auch keine Hochrechnung vornehmen. (Stichwort T-Test)
Wenn du noch weitere statistische Auswertungen mit den dann 8.000 Datensätzen vornehmen möchtest würde ich an deiner Stelle R nutzen. Da sind die Methoden hinterlegt und du musst dir nicht alles selbst bauen.

 

[species_0001]

den Beweis wird man nicht führen können. Die Auswahl wahr gefühlt zufällig. Ob sie in die Normalverteilung passen oder Ausreißer waren würde man erst im Nachhinein, nach der Gesamtzählung, wissen.
aber eigentlich würde ich es Kraft Definition annehmen, dass wir hochrechnen dürfen

 

[_killy_]

Also ich weiß nicht wofür es ist. Wenn du aber nicht nur mit den Zahlen spielen willst, sondern wirklich Erkenntnisse aus diesem ziehen möchtest -> musst du einen T-Test auf Normalverteilung machen.
Ergibt der T-Test eine Normalverteilung, darfst du hochrechnen, ergibt der T-Test keine Normalverteilung wäre das hochrechnen "extrem gefährlich".